��Ŀ����
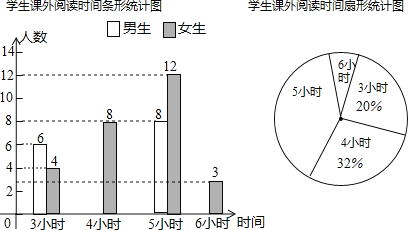
����Ŀ��ij����ѧУΪʹ��һ������У��ʱ���Ϻ�����У��������ǰ��ijУ���꼶��1����ѧ����������У���ͺ�������������飬�����ݵ�����������ͼ������������ͳ��ͼ��У���ͺ���������Ϊ��������Ϊ6���ͺţ���
����������Ϣ������������⣺
��1���ð�ж�����ѧ����
��2��������ͳ��ͼ�У���ѿ�ȱ���ֲ���������������ͳ��ͼ�У������185��У������Ӧ������Բ�ĽǵĴ�С��
��3����ð�ѧ������У���ͺŵ���������λ��������ø���ѧУ������2000����һ�������������Ҫ��������180�ͺŵ�У����
���𰸡���1������50��ѧ������2���𰸼�������14.4������3��������165��170����λ����170��200�ף�
��������
��1������������=165�͵���������Ӧ�İٷֱ���⼴�ɣ�
��2�������175��185�͵�ѧ���������ٲ�ȫͳ��ͼ���ɣ�
��3��������������λ���Ķ��弰2000��180�ͺ���ռ�İٷֱ���⼴�ɣ�
�⣺��1��15��30%=50��������50��20%=10��������
�𣺸ð��50��ѧ�������д�175��У����ѧ����10����
��2����175��У����ѧ����10����50��20%��10��������
185�͵�ѧ������Ϊ��50-3-15-15-10-5=50-48=2��������
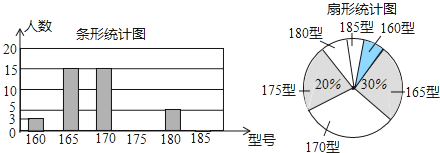
��ȫͳ��ͼ��ͼ��ʾ��
185��У������Ӧ������Բ�Ľ�Ϊ��![]() ��360����14.4����
��360����14.4����
��3��165�ͣ�170��ѧ����࣬��Ϊ15��
��ð�ѧ������У���ͺŵ�����Ϊ165��170��
���ͺŴ�С�������к�25���͵�26��ͬѧ��Ϊ170��
����λ��Ϊ170��
2000![]() ���ף�
���ף�
����Ҫ��200��180�ͺŵ�У����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��С����С����������һ���Ƕȵķ���������ڲ����ǿ��������������£�С��ķ��и߶�y(m)�����ķ���ʱ��x(s)������κ�����ϵ��y��x�ļ����Ӧֵ���±���ʾ��
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | �� |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | �� |
(��)��y����x�ĺ�������ʽ(��Ҫ��дx��ȡֵ��Χ)��
(��)�ʣ�С��ķ��и߶��ܷ�ﵽ22m����˵������.