题目内容
【题目】如图,边长为![]() 的等边
的等边![]() 和边长为
和边长为![]() 的等边
的等边![]() ,它们的边
,它们的边![]() ,
,![]() 位于同一条直线
位于同一条直线![]() 上,开始时,点
上,开始时,点![]() 与点
与点![]() 重合,
重合,![]() 固定不动,然后把
固定不动,然后把![]() 自左向右沿直线
自左向右沿直线![]() 平移,移出
平移,移出![]() 外(点
外(点![]() 与点
与点![]() 重合)停止,设
重合)停止,设![]() 平移的距离为
平移的距离为![]() ,两个三角形重合部分的面积为
,两个三角形重合部分的面积为![]() ,则
,则![]() 关于
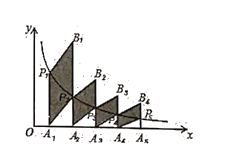
关于![]() 的函数图象是( )
的函数图象是( )
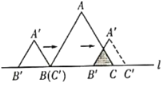
A.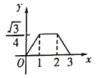 B.
B.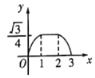 C.
C.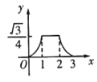 D.
D.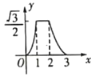
【答案】C
【解析】
分为0≤x≤1、1<x≤2、2<x≤3三种情况画出图形,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
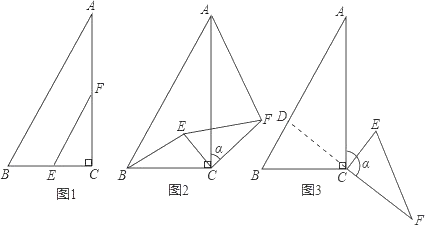
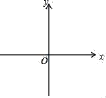
解:如图1所示:当0≤x≤1时,过点D作DE⊥BC′.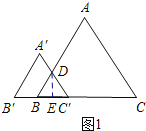
∵△ABC和△A′B′C′均为等边三角形,
∴△DBC′为等边三角形.
∴DE=![]() BC′=
BC′=![]() x,
x,
∴y=![]() BC′DE=
BC′DE=![]() x2.
x2.
当x=1时,y=![]() ,且抛物线的开口向上.
,且抛物线的开口向上.
如图2所示:1<x≤2时,过点A′作A′E⊥B′C′,垂足为E.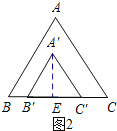
∵y=![]() B′C′A′E=
B′C′A′E=![]() ×1×
×1×![]() =
=![]() .
.
∴函数图象是一条平行与x轴的线段.
如图3所示:2<x≤3时,过点D作DE⊥B′C,垂足为E.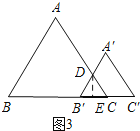
y=![]() B′CDE=
B′CDE=![]() (x-3)2,函数图象为抛物线的一部分,且抛物线开口向上.
(x-3)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:C.

练习册系列答案
相关题目