题目内容
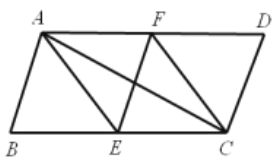
【题目】如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
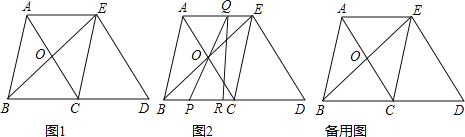
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化.若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段PB的长为何值时,△PQR与△BOC相似.
【答案】(1)菱形,证明见解析;(2)①不变,24;②PB=![]() .
.
【解析】
解:(1)四边形ABCE是菱形.
∵△ECD是由△ABC沿BC平移得到的,
∴EC∥AB,且EC=AB,
∴四边形ABCE是平行四边形,
又∵AB=BC,
∴四边形ABCE是菱形;
(2)①四边形PQED的面积不发生变化.
方法一:∵ABCE是菱形,
∴AC⊥BE,OC=![]() AC=3,
AC=3,
∵BC=5,
∴BO=4,
过A作AH⊥BD于H,(如图1)

∵![]() ,
,
即![]() ,
,
解得AH=![]() .
.
或∵∠AHC=∠BOC=90°,∠BCA=∠BCA,
∴△AHC∽△BOC,
∴AH:BO=AC:BC,
即AH:4=6:5,
∴AH=![]() .
.
由菱形的对称性知,△PBO≌△QEO,
∴BP=QE,
∴![]()
方法二:由菱形的对称性知,△PBO≌△QEO,
∴![]() ,
,
∵△ECD是由△ABC平移得到的,
∴ED∥AC,ED=AC=6,
又∵BE⊥AC,
∴BE⊥ED,
∴![]()
![]()
![]()
![]()
![]()
=24
②方法一:如图2,

当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,
∴∠2>∠3,
∴∠2不与∠3对应,
∴∠2与∠1对应,
即∠2=∠1,
∴OP=OC=3
过O作OG⊥BC于G,则G为PC的中点,
∴△OGC∽△BOC,
∴CG:CO=CO:BC,
即CG:3=3:5,
∴CG=![]() ,
,
∴![]() .
.
方法二:如图3,

当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,
∴∠2>∠3,
∴∠2不与∠3对应,
∴∠2与∠1对应,
∴QR:BO=PR:OC
即![]() :4=PR:3,
:4=PR:3,
∴PR=![]() ,
,
过E作EF⊥BD于F,设PB=x,则RF=QE=PB=x,
DF=![]() ,
,
∴BD=PB+PR+RF+DF=![]() ,
,
解得x=![]() .
.
方法三:如图4,
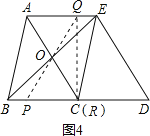
若点P在BC上运动,使点R与C重合,
由菱形的对称性知,O为PQ的中点,
∴CO是Rt△PCQ斜边上的中线,
∴CO=PO,
∴∠OPC=∠OCP,
此时,Rt△PQR∽Rt△CBO,
∴PR:CO=PQ:BC,
即PR:3=6:5,
∴PR=![]()
∴PB=BC﹣PR=![]() .
.