题目内容
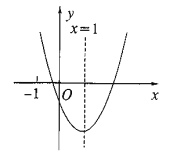
【题目】二次函数
的图象如图所示，对称轴为
．给出以下结论：①
；②
；③
；④
．其中，正确的结论有（ ）
A.
个B.
个C.
个D.
个
【答案】B
【解析】
根据二次函数的图象的开口方向，对称轴以及与y轴的交点位置可判断出a，b，c的取值范围，从而可对①判断；根据抛物线与x轴的交点个数对②进行判断；根据抛物线的对称性确定x=2时y的取值即可对③进行判断；由对称轴x=1可求出b=2a，再根据x=-1结合函数的图象确定y的取值范围即可对④进行判断，从而可求出本题的答案．
①∵函数图象开口向上，
∴a＞0，
∵函数图象与y轴的负半轴相交，
∴c＜0，
∵抛物线的对称轴在y轴的右侧，
∴
，
∴b＞0，
∴abc＜0，故①错误；
②∵函数图象与x轴有两个交点，
∴△=b2-4ac＞0，
∴
，故②正确；
③抛物线上的点（0，y）关于直线x=1对称点的坐标为（2，y），
∵x=0时，y=c＜0，
∴x=2时，y=4a+2b+c＜0，故③错误；
④由对称轴可知：
，
∴b=-2a，
∴当x=-1时，
y=a-b+c＞0，
即3a+c＞0，故④正确；
故选：B．
新非凡教辅冲刺100分系列答案
【题目】某厂家销售一种产品，现准备从网上销售和市场直销两种销售方案中选择一种进行销售．由于受各种不确定因素影响，不同销售的方案会产生不同的成本和其它费用．设每月销售x件，网上销售月利润为w网（元），市场直销月利润为w市（元），具体信息如表：
每件售价（元） | 每件成本（元） | 月其他费用（元） | |
网上销售 | - | 20 | 45000 |
市场直销 | 120 | k |
|
其中k为常数，且30≤k≤50．月利润=月销售额-月成本-月其它费用．
（1）当x=500时，网上销售单价为______元．
（2）分别求出w网，w市与x间的函数解析式（不必写x的取值范围）．
（3）若网上销售月利润的最大值与市场直销月利润的最大值相同，求k的值．
（4）如果某月要将3000件产品全部销售完，请你通过分析帮厂家做出决策，选择在网上销售还是市场直销才能使月利润较大？
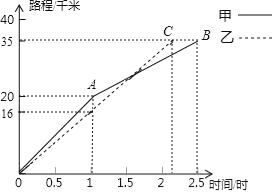
【题目】为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用下面的折线统计图表示：（甲为实线，乙为虚线）
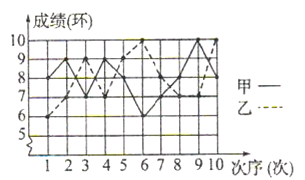
（1）依据折线统计图，得到下面的表格：
射击次序（次） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩（环） | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩（环） | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中
________，
________；
（2）甲成绩的众数是________环，乙成绩的中位数是________环；
（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？
（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率.
