Question

【题目】已知：抛物线 y＝ax2＋bx＋1 经过 A(1，0)、B(－1，3)两点．

（1）求 a，b 的值；

（2）以线段 AB 为边作正方形 ABB′A′，能否将已知抛物线平移，使其经过 A′、B′两点？若能，求出平移后经过 A′、B′两点的抛物线的解析式；若不能，请说明理由．

Answer 1

【答案】（1），；（2）能，抛物线解析式为：或.

【解析】

（1）根据题意将A、B两点坐标代入解析式进一步求解即可；

（2）如图，根据题意，首先画出合适的图形，得出正方形ABB′A′以及ABB′′A′′，然后根据两种图形分两种情况进一步分析讨论即可.

（1）∵抛物线 y＝ax2＋bx＋1 经过 A(1，0)、B(－1，3)两点，

故有：，，

∴，；

（2）

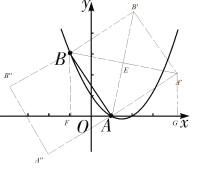
连接A′B，AB′交于点E，过点B作BF⊥x轴于点F，过点A′作A′G⊥x轴于点G，

∵四边形ABB′A′为正方形，

∴∠BA A′=90°，AB= A′A，BE= A′E= B′E=AE，

∵∠BA A′=90°，

∴∠BAF+∠A′AG=90°，

∵∠ABF+∠BAF=90°，

∴∠A′AG=∠ABF，

在△BAF与△A′AG中，

∵∠BFA=∠AG A′，∠ABF=∠A′AG，AB= A′A，

∴△BAF≌△A′AG，

∴A′G=AF，AG=BF，

∵AF=2，BF=3，

∴点A′的横坐标=OG=OA+AG=4，

点A′的纵坐标= A′G=2，

即点A′的坐标为(4，2)，

∵点A′的坐标为(4，2)，点B的坐标为(，3)，E是A′B的中点，

∴点E的坐标为：(，)，

∵E是A B′的中点，点A的坐标为(1，0)，

∴点B′的横坐标=，点B′的纵坐标=，

即点B′的坐标为(2，5)，

过A、B两点的抛物线的解析式为：，

化为顶点式为：，

设平移后的解析式为：，

假设其经过点A′、B′，

则：，

，

∴，，

故存在经过A′、B′两点的抛物线，其解析式为：，

当正方形为ABB′′A′′时，同理可得点A′′的坐标为(，)，点B′′的坐标为(，1)，

此时经过A′′、B′′两点的抛物线的解析式为：.