题目内容
【题目】如图,在△ABC 中,D、E、F 分别为边 AB、AC、BC 上的点,连接 DE、EF.若 DE∥BC,EF∥AB,则图中共有________对相似三角形.
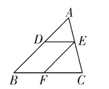
【答案】3
【解析】
首先根据DE∥BC可以得出∠ADE=∠B,∠AED=∠C,然后根据EF∥AB可以得出∠FEC=∠A,∠EFC=∠B,利用以上条件再结合相似三角形判定定理进一步求解即可.
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∵EF∥AB,
∴∠FEC=∠A,∠EFC=∠B,
在△ADE与△ABC中,
∵∠A=∠A,∠ADE=∠B,
∴△ADE~△ABC,
在△ADE与△EFC中,
∵∠FEC=∠A,∠AED=∠C,
∴△ADE~△EFC,
在△ABC与△EFC中,
∵∠FEC=∠A,∠C=∠C,
∴△ABC~△EFC,
综上所述,共有三对相似三角形,
故答案为:3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目