题目内容
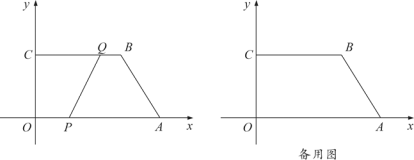
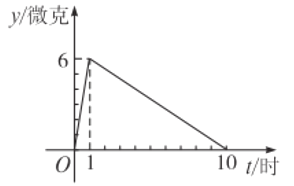
【题目】在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间的关系近似地满足图中折线.
(小时)之间的关系近似地满足图中折线.
(1)求注射药物后每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
【答案】(1)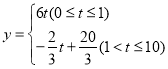 ;(2)
;(2)![]() (小时)
(小时)
【解析】
(1)当0≤t≤1时,是正比例函数,用待定系数法进行求解,即可,当1<t≤10时,是一次函数,用待定系数法求函数的关系式,即可;
(2)当0≤t≤1时,当含药量上升到4微克时,控制病情开始有效,令y=4,代入y=6t,求出对应的t值,同理,当1<t≤10时,求出另一个t值,他们的差就是药的有效时间.
(1)当0≤t≤1时,设y=k1t,则6=k1×1,
∴k1=6,
∴y=6t.
当1<t≤10时,设y=k2t+b,
∴![]() ,解得:
,解得: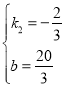 ,
,
∴ y=![]() t+
t+![]() ,
,
综上所述: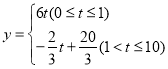 ;
;
(2)当0≤t≤1时,令y=4,即:6t=4,解得:t=![]() ,
,
当0<t≤10时,令y=4,即:![]() t+
t+![]() =4,解得:t=4,
=4,解得:t=4,
∴控制病情的有效时间为:4![]() =
=![]() (小时).
(小时).

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目