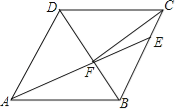
题目内容
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的是 (把所有正确结论的序号都填在横线上).
.其中一定成立的是 (把所有正确结论的序号都填在横线上).
【答案】①②③
【解析】
试题∵ 四边形ABCD是菱形,∴AB=BC=6,
∵∠DAB=60°,∴AB=AD=DB,∠ABD=∠DBC=60°,
在△ABF与△CBF中,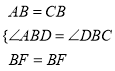 ,
,
∴△ABF≌△CBF(SAS),
∴①正确;
过点E作EG⊥AB,过点F作MH⊥CD,MH⊥AB,如图:
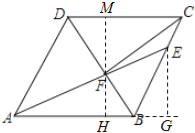
∵CE=2,BC=6,∠ABC=120°,
∴BE=6﹣2=4,
∵EG⊥AB,
∴EG=![]() ,
,
∴点E到AB的距离是![]() ,
,
故②正确;
∵BE=4,EC=2,
∴S△BFE:S△FEC=4:2=2:1,
∴S△ABF:S△FBE=3:2,
∴△ABF的面积为=![]() ,
,
故④错误;
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴FM=![]() ,
,
∴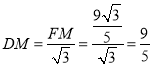 ,
,
∴CM=DC﹣DM=6﹣![]() =
=![]() ,
,
∴tan∠DCF=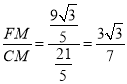 ,
,
故③正确;
故答案为①②③

【题目】为了了解学生对“预防新型冠状病毒”知识的掌握情况,学校组织了一次线上知识培训,培训结束后进行测试,在全校2000名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
15名男生测试成绩统计如下:(满分100分)78,90,99,93,92,95,94,100,90,85,86,95,75,88,90
15名女生测试成绩统计如下:(满分100分)77,82,83,86,90,90,92,91,93,92,92,92,92,98,100
(整理、描述数据)
70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 | 95.5~100.5 | |
男生 | 1 | 1 | 1 | 5 | 5 | 2 |
女生 | 0 | 1 | 2 | 3 | 7 | 2 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
性别 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 90 | 90 | 90 | 44.9 |
女生 | 90 |
|
| 32.8 |
在表中:![]() ________.
________.![]() ________;
________;
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中“预防新型冠状病毒”知识测试合格的学生有多少人?
(3)通过数据分析得到的结论,你认为男生和女生中谁的成绩比较好?请说明理由.
【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.