Question

【题目】如图，在等腰直角三角形中，，点为中点，点为外一点，已知，则CD的长为（ 　）

A.B.C.D.

Answer 1

【答案】A

【解析】

过点B作BF⊥CE交CE的延长线于点F，由∠BEC=135°，得∠BEF=45°，再通过解直角三角形BEF求得BF、EF的长，进而可求得BC长，在等腰直角三角形中，再通过解直角三角形求得AB长，最后利用斜边上的中线等于斜边一半求得CD长即可．

解：如图，过点B作BF⊥CE交CE的延长线于点F，

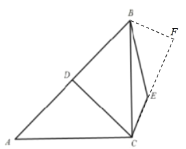
∵∠BEC=135°，

∴∠BEF=180°-135°=45°，

在Rt△BEF中，sin∠BEF=，cos∠BEF=，

∴BF=BE·sin∠BEF=，EF=BE·cos∠BEF=，

又∵EC=，

∴CF=EC+EF=2，

在Rt△BEF中，BC2=BF2+CF2，

则BC=，

∵在等腰直角三角形中，∠A=45°，sinA=，

∴，

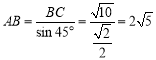∵在直角三角形中，点为中点，

∴CD=AB=，

故选：A．