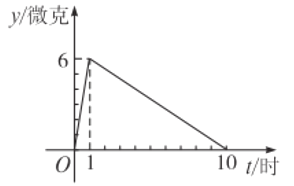
题目内容
【题目】如图,在△ABC中,DE∥BC,EF∥AB,则下列结论正确的是( )
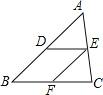
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据相似三角形的判定与性质逐项分析即可.由△ADE∽△ABC,可判断A的正误;由△CEF∽△CAB,可判定B错误;由△ADE~△EFC,可判定C正确;由△CEF∽△CAB,可判定D错误.
解:如图所示:
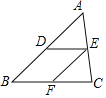
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴![]() ,
,
∴答案A错舍去;
∵EF∥AB,
∴△CEF∽△CAB,
![]()
∴答案B舍去
∵∠ADE=∠B,∠CFE=∠B,
∴∠ADE=∠CFE,
又∵∠AED=∠C,
∴△ADE~△EFC,
∴![]() ,C正确;
,C正确;
又∵EF∥AB,
∴∠CEF=∠A,∠CFE=∠B,
∴△CEF∽△CAB,
∴![]() ,
,
∴答案D错舍去;
故选C.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目