Question

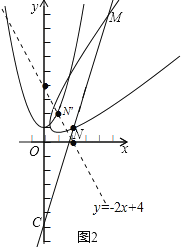
【题目】如图1，已知抛物线的顶点坐标为（0，1）且经过点A（1，2），直线y＝3x﹣4经过点B（，n），与y轴交点为C．

（1）求抛物线的解析式及n的值；

（2）将直线BC绕原点O逆时针旋转45°，求旋转后的直线的解析式；

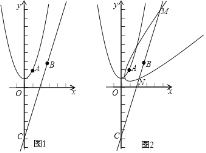
（3）如图2将抛物线绕原点O顺时针旋转45°得到新曲线，新曲线与直线BC交于点M、N，点M在点N的上方，求点N的坐标．

Answer 1

【答案】（1）y＝x2+1，n＝2；（2）y＝﹣2x+4；（3）N（，）．

【解析】

（1）抛物线的表达式为：y＝ax2+1，将点A坐标代入上式得：2＝a+1，即可求解；

（2）点B围绕点O逆时针旋转45°，落在y轴上，设为点B′（0，4），同理点C（0，﹣4）围绕点O逆时针旋转45°，设旋转后该点对应点C′（4，﹣4），即可求解；

（3）在图2中，作直线y＝﹣2x+4交抛物线于点N′，则抛物线和直线y＝﹣2x+4绕原点O顺时针旋转45°得到新曲线和直线线y＝3x﹣4，由ON＝ON′，即可求解．

解：（1）抛物线的表达式为：y＝ax2+1，

将点A坐标代入上式得：2＝a+1，解得：a＝1，

故抛物线的表达式为：y＝x2+1，

n＝3×2﹣4＝2；

（2）∵点B的横坐标和纵坐标相同，BO＝4，

故点B围绕点O逆时针旋转45°，落在y轴上，设为点B′（0，4），

同理点C（0，﹣4）围绕点O逆时针旋转45°，设旋转后该点对应点C′（4，﹣4），

将BC坐标代入一次函数表达式：y＝mx+n得：，解得：，

故旋转后直线的表达式为：y＝﹣2x+4；

（3）在图2中，作直线y＝﹣2x+4交抛物线于点N′，

则抛物线和直线y＝﹣2x+4绕原点O顺时针旋转45°得到新曲线和直线线y＝3x﹣4，

联立y＝x2+1与y＝﹣2x+4并解得：x＝1或﹣3（舍去﹣3），故点N′（1，2），

设点N（m，3m﹣4），

由题意得：ON＝ON′，

即：，解得：m＝（不合题意值已舍去），

故点N′（，）．