��Ŀ����
����Ŀ����ABC����CDE���ǵ��������Σ���BAC����EDC��120����
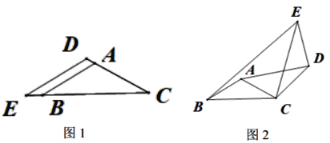
��1����ͼ1��A��D��C��ͬһֱ����ʱ��![]() ��_______��
��_______��![]() ��_______��
��_______��
��2����ͼ1�Ļ����ϣ��̶���ABC������CDE��C��תһ���ĽǶ���(0��������360��)����ͼ2������AD��BE��
�� ![]() ��ֵ��û�иı䣿��˵�����ɣ�
��ֵ��û�иı䣿��˵�����ɣ�
����չ�о�����AB��1��DE��![]() ���� B��D��E��ͬһֱ����ʱ��������߶�AD�ij���
���� B��D��E��ͬһֱ����ʱ��������߶�AD�ij���
���𰸡���1��![]() ��
��![]() ����2����û�иı䣬���ɼ����������߶�AD�ij�Ϊ
����2����û�иı䣬���ɼ����������߶�AD�ij�Ϊ![]() ��
��![]() ��
��
��������
��1���ɵ��������ε����ʺ�ֱ�������ε����ʿɵ�AC��2AH��CH��![]() AH����ƽ���߷��߶γɱ����ɵ�
AH����ƽ���߷��߶γɱ����ɵ�![]() ��������⣻
��������⣻
��2����ͨ��֤����ACD�ס�BCE���ɵ�![]() ���ڷ���������������ۣ���i����ͼ����B��D��E��ͬһֱ���ϣ��ҵ�D��BE�м�ʱ������C��CN��BE��N������ֱ�������ε����ʺ��ɶ������BE��
���ڷ���������������ۣ���i����ͼ����B��D��E��ͬһֱ���ϣ��ҵ�D��BE�м�ʱ������C��CN��BE��N������ֱ�������ε����ʺ��ɶ������BE��![]() ���ɢٵĽ��ۿ���⣻��ii����ͼ���� B��D��E��ͬһֱ���ϣ��ҵ�B��ED�м�ʱ������B��BH��EC��H�����ù��ɶ������BH��
���ɢٵĽ��ۿ���⣻��ii����ͼ���� B��D��E��ͬһֱ���ϣ��ҵ�B��ED�м�ʱ������B��BH��EC��H�����ù��ɶ������BH��![]() �����ɢٵĽ��ۿ���⣮
�����ɢٵĽ��ۿ���⣮
�⣺��1����ͼ1������A��AH��BC��H��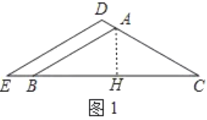
�ߡ�BAC��120����AB��AC��AH��BC��
���ABC����ACB��30����BH��CH��
��AC��2AH��CH��![]() ��
��
��BC��2![]() AH��
AH��
�ߡ�BAC����EDC��120����
��AB��DE��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��2����û�иı䣬
�������£��߽���CDE��C��תһ���ĽǶ�����0��������360������
���ACD����BCE��
��AB��AC��DE��CD��
��![]() ���ҡ�BAC����EDC��120����
���ҡ�BAC����EDC��120����
���ABC�ס�DEC��
��![]() ���ҡ�ACD����BCE��
���ҡ�ACD����BCE��
���ACD�ס�BCE��
��![]() ��
��
��![]() ��ֵ��û�иı�
��ֵ��û�иı�
�ڣ�i����ͼ����B��D��E��ͬһֱ���ϣ��ҵ�D��BE�м�ʱ������C��CN��BE��N��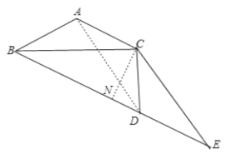
��AC��AB��1��
���ɣ�1����֪��BC��![]() ��
��
�ߡ�CDE��120����
���BDC��60������CD��DE��![]() ��CN��BE��
��CN��BE��
��DN��![]() CD��
CD��![]() ��CN��
��CN��![]() ��
��![]() ��
��
��EC=2CN=![]() ��
��
��BN��![]() ��
��
��BE��![]() ��
��
��![]() ��
��
��AD��![]() ��
��
��ii����ͼ���� B��D��E��ͬһֱ���ϣ��ҵ�B��ED�м�ʱ������B��BH��EC��H��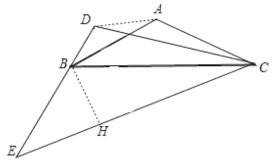
�ߡ�BEC��30����BH��EC��
��BE=2BH��EH��![]() ��
��
��BC2��BH2��HC2��
��3��BH2��![]() ��
��
��BH��![]() ��
��
��BE��![]()
��![]()
��AD��![]() ��
��
�����������߶�AD�ij�Ϊ![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ���˽�ѧ���ԡ�Ԥ������״������֪ʶ�����������ѧУ��֯��һ������֪ʶ��ѵ����ѵ��������в��ԣ���ȫУ2000��ѧ���У��ֱ��ȡ��������Ů����15�ݳɼ������������������£��벹��������
���ռ����ݣ�
15���������Գɼ�ͳ�����£�������100�֣�78��90��99��93��92��95��94��100��90��85��86��95��75��88��90
15��Ů�����Գɼ�ͳ�����£�������100�֣�77��82��83��86��90��90��92��91��93��92��92��92��92��98��100
���������������ݣ�
70.5��75.5 | 75.5��80.5 | 80.5��85.5 | 85.5��90.5 | 90.5��95.5 | 95.5��100.5 | |
���� | 1 | 1 | 1 | 5 | 5 | 2 |
�� | 0 | 1 | 2 | 3 | 7 | 2 |
���������ݣ�
��1�������������ݵ�ƽ��������������λ�����������±���ʾ��
�Ա� | ƽ���� | ���� | ��λ�� | ���� |
���� | 90 | 90 | 90 | 44.9 |
�� | 90 |
|
| 32.8 |
�ڱ��У�![]() ________��
________��![]() ________��
________��
��2�����涨�÷���80�����ϣ�����80�֣�Ϊ�ϸ������ȫУѧ���С�Ԥ������״������֪ʶ���Ժϸ��ѧ���ж����ˣ�
��3��ͨ�����ݷ����õ��Ľ��ۣ�����Ϊ������Ů����˭�ijɼ��ȽϺã���˵�����ɣ�