题目内容
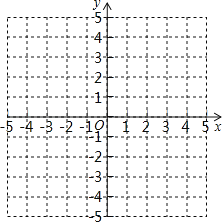
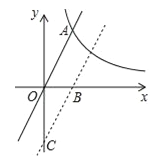
【题目】已知：如图，在平面直角坐标系xOy中，反比例函数
的图象与正比例函数y=kx（k≠0）的图象相交于横坐标为2的点A，平移直线OA，使它经过点B（3，0），与y轴交于点C．
（1）求平移后直线的表达式；
（2）求∠OBC的余切值．
【答案】（1）y=2x﹣6；（2）
．
【解析】
试题分析：（1）根据点A在反比例函数图象上可求出点A的坐标，进而可求出正比例函数表达式，根据平移的性质可设直线BC的函数解析式为y=2x+b，根据点B的坐标利用待定系数法即可求出b值，此题得解；
（2）利用一次函数图象上点的坐标特征即可求出点C的坐标，从而得出OC的值，再根据余切的定义即可得出结论．
试题解析：（1）当x=2时，y=
=4，∴点A的坐标为（2，4）．
∵A（2，4）在y=kx（k≠0）的图象上，∴4=2k，解得：k=2．
设直线BC的函数解析式为y=2x+b，∵点B的坐标为（3，0），∴0=2×3+b，解得：b=﹣6，∴平移后直线的表达式y=2x﹣6．
（2）当x=0时，y=﹣6，∴点C的坐标为（0，﹣6），∴OC=6，∴cot∠OBC=
=
=
．
练习册系列答案
智慧小复习系列答案
相关题目
