Question

【题目】如图，已知A（﹣2，4），B（4，2），C（2，﹣1）

（1）作△ABC关于x轴的对称图形△A1B1C1，写出点C关于x轴的对称点C1的坐标；

（2）P为x轴上一点，请在图中画出使△PAB的周长最小时的点P并直接写出此时点P的坐标（保留作图痕迹）．

Answer 1

【答案】详见解析.

【解析】试题分析：

(1) 先根据题目给出的已知点的坐标，在图中的相应位置上标出原三角形的三个顶点. 根据关于x轴对称的点的坐标规律，将对称变换后的三角形的顶点坐标写出，即A1 (-2, -4)，B1 (4, -2)，C1 (2, 1). 在图中相应的位置上标出对称变换后的三角形的三个顶点. 连接这三个顶点即得所求的△A1B1C1. 至于题目中有关写出点C1坐标的问题，可以根据前面得到的点C1的坐标作答即可.

(2) △PAB的周长为PA+PB+AB. 由于点A和点B均为坐标已知的固定点，所以线段AB的长度是一个定值. 因此，△PAB的周长最小就是PA+PB最小. 这种最小值问题可以利用轴对称进行求解. 先将点A关于x轴的对称点A1画出：过点A作x轴的垂线(为叙述方便，设垂足为点D)，在线段AD的延长线上截取DA1=DA，则点A1即为点A关于x轴的对称点. 然后，连接A1B，交x轴于点P，则点P即为所求. 观察图形不难看出，点P的坐标为(2, 0).

试题解析：

(1) 如图所示，△A1B1C1即为所求.

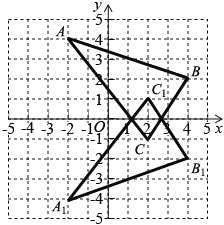
∵点C与点C1关于x轴对称，

又∵点C的坐标为(2, -1)，

∴点C1的坐标为(2, 1).

(2) 如图所示，点P即为所求.

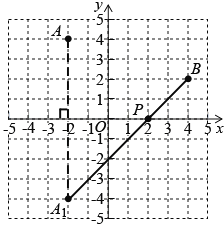
根据上述图形可知，点P的坐标为(2, 0).