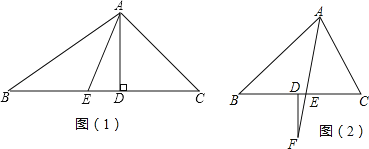题目内容
【题目】已知△ABC中,∠A=50°.
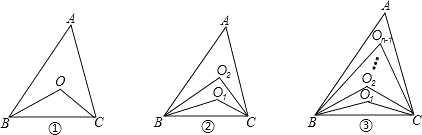
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC= °.
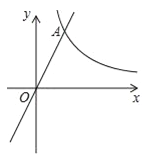
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2,则∠BO2C= °.
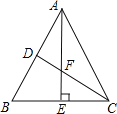
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示).
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1,若∠BOn﹣1C=60°,求n的值.
【答案】(1)、115°;(2)、![]() ;(3)、﹣
;(3)、﹣![]() ×130°;(4)、n=13.
×130°;(4)、n=13.
【解析】
试题分析:(1)、△ABC中,已知∠A即可得到∠ABC与∠ACB的和,而BO、CO是∠ABC,∠ACB的两条角平分线,即可求得∠OBC与∠OCB的度数,根据三角形的内角和定理即可求解;(2)、先根据三角形内角和定理求得∠ABC+∠ACB,再根据三等分线的定义求得∠O2BC+∠O2CB,即可求出∠BO2C;
(3)、先根据三角形内角和定理求得∠ABC+∠ACB,再根据n等分线的定义求得∠On﹣1BC+∠On﹣1CB,即可求出∠BOn﹣1C.(4)、依据(3)的结论即可求出n的值.
试题解析:(1)、∵△ABC中,∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,BO、CO是∠ABC,∠ACB的两条角平分线. ∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB, ∴∠OBC+∠OCB=
∠ACB, ∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=65°,
(∠ABC+∠ACB)=65°,
∴△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=115° (2)、∵点O2是∠ABC与∠ACB的三等分线的交点,
∴∠O2BC+∠O2CB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°=(
×130°=(![]() )°,
)°,
∴∠BO2C=180°﹣(![]() )°=(
)°=(![]() )°.
)°.
(3)、∵点On﹣1是∠ABC与∠ACB的n等分线的交点,
∴∠On﹣1BC+∠On﹣1CB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×130°, ∴∠BOn﹣1C=180°﹣
×130°, ∴∠BOn﹣1C=180°﹣![]() ×130°;
×130°;
(4)、∵∠BOn﹣1C=60°, ∴180°﹣![]() ×130°=60°,解得n=13.
×130°=60°,解得n=13.