Question

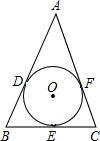
已知在△ABC中，AB=AC=13，BC=10，那么△ABC的内切圆的半径为（　　）

A． 10 3

B． 12 5

C．2

D．3

Answer 1

连OA，OB，OC．因为AB=AC，O是内心，所以AO⊥BC，垂足为F．
设内切圆半径为r，
∵AB=AC=13，BC=10，
∴BF=5，
∴AF=12，则S_△ABC=

1

2

×12×10=60；
又∵S_△ABC=S_△OAC+S_△OBC+S_△OAC=

1

2

rAB+

1

2

rAC+

1

2

rBC=

1

2

r（13+13+10）=60，
∴r=

10

3

．
故选A．