题目内容
【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)求△MCB的面积.

【答案】(1)y=﹣x2+4x+5;(2)y=﹣x+5;(3)15.
【解析】
(1)由A、C、(1,8)三点在抛物线上,根据待定系数法即可求出抛物线的解析式;
(2)由B、C两点的坐标求得直线BC的解析式;
(3)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=![]()
(1)∵A(﹣1,0),C(0,5),(1,8)三点在抛物线y=ax2+bx+c上,
∴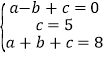 ,
,
解方程组,得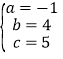 ,
,
故抛物线的解析式为y=﹣x2+4x+5;
(2)∵y=﹣x2+4x+5=﹣(x﹣5)(x+1)=﹣(x﹣2)2+9,
∴M(2,9),B(5,0),
设直线BC的解析式为:y=kx+b,
![]()
解得,![]()
则直线BC的解析式为:y=﹣x+5;
(3)过点M作MN∥y轴交BC轴于点N,
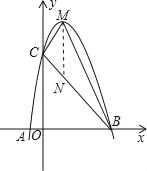
则△MCB的面积=△MCN的面积+△MNB的面积=![]()
当x=2时,y=﹣2+5=3,则N(2,3),
则MN=9﹣3=6,
则![]()

练习册系列答案
相关题目