题目内容
【题目】如图，点
是正方形
的边
上的一点，
，正方形的边长为8．则
的长为__________．
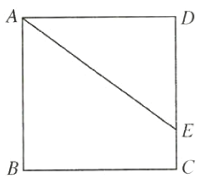
【答案】6
【解析】
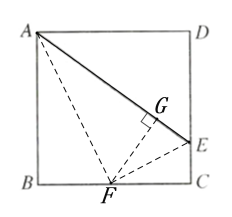
作∠BAE的角平分线交BC于点F，过F作FG⊥AE，连接EF，结合正方形的性质和全等三角形的性质可得CE=GE，在RtΔADE中根据勾股定理列方程求解.
解：作∠BAE的角平分线交BC于点F，过F作FG⊥AE，垂足为G，连接EF，
∵四边形ABCD是正方形，
∴AB=BC=CD=DA, ∠B=∠C=∠D=90°
∵∠ABF=∠AGF=90°,∠BAF=∠GAF，AF=AF，
∴ΔABF≌ΔAGF，
∴AG=AB.
∵AE=BC+CE，AE=AG+GE，AB=AG=BC
∴CE=GE，
设DE=x，则CE=EG=8-x
在RtΔADE中，由勾股定理得，
∴
解得，x=6
∴DE=6.
故答案为：6
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
