题目内容
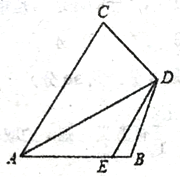
【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
【答案】C
【解析】分析:根据AD=AB和三角形内角和、外角性质,寻找∠C和∠BAC的关系的表达式;再根据BE=BC,寻找∠C和∠BAC关系的另一种表达式,由此可得关于∠BAC的方程,求得的度数,代入即可求得∠C.
详解:
∵AD=AB,
∴∠ADB=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC,
∠BAC,
∴∠C=∠ADB﹣∠DAC=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC﹣
∠BAC﹣![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() ∠BAC;
∠BAC;
∵BE=BC,
∴∠C=∠BEC=∠BAC+∠ABE=∠BAC+![]() (180°﹣
(180°﹣![]() ∠BAC)=∠BAC+45°﹣
∠BAC)=∠BAC+45°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
∴90°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
解得∠BAC=![]() ,
,
∴∠C=90°﹣![]() .
.
故选C.

练习册系列答案
相关题目