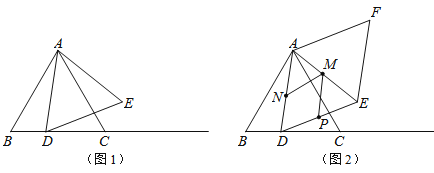ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏy=ax2+bx©¹2”κx÷αΫΜ”ΎΒψAΘ®©¹1Θ§0Θ©Θ§BΘ®4Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§Ψ≠ΙΐΒψBΒΡ÷±œΏΫΜy÷α”ΎΒψEΘ®0Θ§2Θ©Θ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
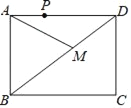
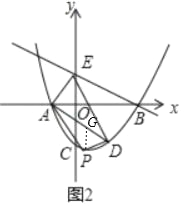
Θ®2Θ©»γΆΦ2Θ§ΙΐΒψAΉςBEΒΡΤΫ––œΏΫΜ≈ΉΈοœΏ”ΎΝμ“ΜΒψDΘ§ΒψP «≈ΉΈοœΏ…œΈΜ”ΎœΏΕΈADœ¬ΖΫΒΡ“ΜΗωΕ·ΒψΘ§Ν§ΫαPAΘ§EAΘ§EDΘ§PDΘ§«σΥΡ±Ώ–ΈEAPDΟφΜΐΒΡΉν¥σ÷ΒΘΜ
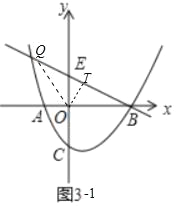
Θ®3Θ©»γΆΦ3Θ§Ν§ΫαACΘ§ΫΪΓςAOC»ΤΒψOΡφ ±’κΖΫœρ–ΐΉΣΘ§Φ«–ΐΉΣ÷–ΒΡ»ΐΫ«–ΈΈΣΓςAΓδOCΓδΘ§‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§÷±œΏOCΓδ”κ÷±œΏBEΫΜ”ΎΒψQΘ§»τΓςBOQΈΣΒ»―ϋ»ΐΫ«–ΈΘ§«κ÷±Ϋ”–¥≥ωΒψQΒΡΉχ±ξΘ°

ΓΨ¥πΑΗΓΩΘ®1Θ©y=![]() x2©¹
x2©¹![]() x©¹2ΘΜΘ®2Θ©9ΘΜΘ®3Θ©QΉχ±ξΈΣΘ®©¹
x©¹2ΘΜΘ®2Θ©9ΘΜΘ®3Θ©QΉχ±ξΈΣΘ®©¹![]() Θ©ΜρΘ®4©¹
Θ©ΜρΘ®4©¹![]() Θ©ΜρΘ®2Θ§1Θ©ΜρΘ®4+
Θ©ΜρΘ®2Θ§1Θ©ΜρΘ®4+![]() Θ§©¹
Θ§©¹![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ ![]() Α―Βψ
Α―Βψ![]() ¥ζ»κ≈ΉΈοœΏ
¥ζ»κ≈ΉΈοœΏ![]() Θ§«σ≥ω
Θ§«σ≥ω![]() ΒΡ÷ΒΦ¥Ω….
ΒΡ÷ΒΦ¥Ω….
![]() œ»”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏBEΒΡΫβΈω ΫΘ§ΫχΕχ«σΒΟ÷±œΏADΒΡΫβΈω ΫΘ§…η
œ»”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏBEΒΡΫβΈω ΫΘ§ΫχΕχ«σΒΟ÷±œΏADΒΡΫβΈω ΫΘ§…η![]() ‘ρ
‘ρ![]() ±μ Ψ≥ω
±μ Ψ≥ω![]() ,”Ο≈δΖΫΖ®«σ≥ωΥϋΒΡΉν¥σ÷ΒΘ§
,”Ο≈δΖΫΖ®«σ≥ωΥϋΒΡΉν¥σ÷ΒΘ§
ΝΣΝΔΖΫ≥Χ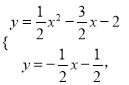 «σ≥ωΒψ
«σ≥ωΒψ![]() ΒΡΉχ±ξΘ§
ΒΡΉχ±ξΘ§ ![]() Ήν¥σ÷Β=
Ήν¥σ÷Β=![]() Θ§
Θ§
ΫχΕχΦΤΥψΥΡ±Ώ–ΈEAPDΟφΜΐΒΡΉν¥σ÷ΒΘΜ
![]() Ζ÷ΝΫ÷÷«ιΩωΫχ––Χ÷¬έΦ¥Ω….
Ζ÷ΝΫ÷÷«ιΩωΫχ––Χ÷¬έΦ¥Ω….
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏ![]() ‘Ύ≈ΉΈοœΏ
‘Ύ≈ΉΈοœΏ![]() …œΘ§
…œΘ§
Γύ![]()
ΫβΒΟ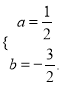
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]()
Θ®2Θ©ΙΐΒψPΉς![]() ÷αΫΜAD”ΎΒψGΘ§
÷αΫΜAD”ΎΒψGΘ§
ΓΏ![]()
Γύ÷±œΏBEΒΡΫβΈω ΫΈΣ![]()
ΓΏADΓΈBEΘ§…η÷±œΏADΒΡΫβΈω ΫΈΣ![]() ¥ζ»κ
¥ζ»κ![]() Θ§Ω…ΒΟ
Θ§Ω…ΒΟ![]()
Γύ÷±œΏADΒΡΫβΈω ΫΈΣ![]()
…η![]() ‘ρ
‘ρ![]()
‘ρ![]()
ΓύΒ±x=1 ±Θ§PGΒΡ÷ΒΉν¥σΘ§Ήν¥σ÷ΒΈΣ2Θ§
”…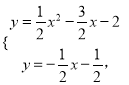 ΫβΒΟ
ΫβΒΟ![]() Μρ
Μρ![]()
Γύ![]()
Γύ![]() Ήν¥σ÷Β=
Ήν¥σ÷Β=![]()
![]()
ÿADøBEȧ
Γύ![]()
ΓύSΥΡ±Ώ–ΈAPDEΉν¥σ=SΓςADPΉν¥σ+![]()
Θ®3Θ©ΔΌ»γΆΦ3©¹1÷–Θ§Β±![]() ±Θ§Ής
±Θ§Ής![]() ”ΎTΘ°
”ΎTΘ°
ΓΏ![]()
Γύ![]()
Γύ![]()
Γύ![]()
Ω…ΒΟ![]()
ΔΎ»γΆΦ3©¹2÷–Θ§Β±![]() ±,
±, 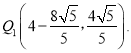
Β±![]() ±Θ§
±Θ§ ![]()
Β±![]() ±Θ§Q3
±Θ§Q3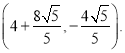
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒψΒψQΉχ±ξΈΣ![]() Μρ
Μρ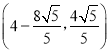 Μρ
Μρ![]() Μρ
Μρ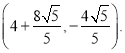

 Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ–ΓΆθΆ§―ß‘Ύ―ß–ΘΉι÷·ΒΡ…γΜαΒς≤ιΜνΕ·÷–ΗΚ‘πΝΥΫβΥϊΥυΨ”ΉΓΒΡ–Γ«χ450ΜßΨ”ΟώΒΡ…ζΜν”ΟΥ°«ιΩωΘ§Υϊ¥”÷–ΥφΜζΒς≤ιΝΥ50ΜßΨ”ΟώΒΡ‘¬Ψυ”ΟΥ°ΝΩΘ®ΒΞΈΜΘΚtΘ©Θ§≤ΔΜφ÷ΤΝΥ―υ±ΨΒΡΤΒ ΐΖ÷≤Φ±μΚΆΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ®»γΆΦΘ©Θ°
‘¬Ψυ”ΟΥ°ΝΩΘ®ΒΞΈΜΘΚtΘ© | ΤΒ ΐ | ΑΌΖ÷±» |
2ΓήxΘΦ3 | 2 | 4% |
3ΓήxΘΦ4 | 12 | 24% |
4ΓήxΘΦ5 | ΓΓ ΓΓ | ΓΓ ΓΓ |
5ΓήxΘΦ6 | 10 | 20% |
6ΓήxΘΦ7 | ΓΓ ΓΓ | 12% |
7ΓήxΘΦ8 | 3 | 6% |
8ΓήxΘΦ9 | 2 | 4% |
Θ®1Θ©«κΗυΨίΧβ÷–“―”–ΒΡ–≈œΔ≤Ι»ΪΤΒ ΐΖ÷≤Φ±μΚΆΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘΜ
Θ®2Θ©»γΙϊΦ“ΆΞ‘¬Ψυ”ΟΥ°ΝΩΓΑ¥σ”ΎΜρΒ»”Ύ4t«“–Γ”Ύ7tΓ±ΈΣ÷–Β»”ΟΥ°ΝΩΦ“ΆΞΘ§«κΡψΙάΦΤΉήΧε–ΓΆθΥυΨ”ΉΓΒΡ–Γ«χ÷–Β»”ΟΥ°ΝΩΦ“ΆΞ¥σ‘Φ”–Εύ…ΌΜßΘΩ
Θ®3Θ©¥”‘¬Ψυ”ΟΥ°ΝΩ‘Ύ2ΓήxΘΦ3Θ§8ΓήxΘΦ9’βΝΫΗωΖΕΈßΡΎΒΡ―υ±ΨΦ“ΆΞ÷–»Έ“β≥ι»Γ2ΗωΘ§«κ”ΟΝ–ΨΌΖ®Θ®Μ≠ ςΉ¥ΆΦΜρΝ–±μΘ©«σ≥ι»Γ≥ωΒΡ2ΗωΦ“ΆΞά¥Ή‘≤ΜΆ§ΖΕΈßΒΡΗ≈¬ Θ°

ΓΨΧβΡΩΓΩΈΣΝΥΫβΡ≥ – –ΟώΓΑ¬Χ…Ϊ≥ω––Γ±ΖΫ ΫΒΡ«ιΩωΘ§Ρ≥–Θ ΐ―ß–Υ»Λ–ΓΉι“‘Έ ΨμΒς≤ιΒΡ–Έ ΫΘ§ΥφΜζΒς≤ιΝΥΡ≥ –≤ΩΖ÷≥ω–– –ΟώΒΡ÷ς“Σ≥ω––ΖΫ ΫΘ®≤Έ”κΈ ΨμΒς≤ιΒΡ –ΟώΕΦ÷Μ¥”“‘œ¬ΈεΗω÷÷άύ÷–―Γ‘ώ“ΜάύΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γœ¬≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°
÷÷άύ | A | B | C | D | E |
≥ω––ΖΫ Ϋ | Ι≤œμΒΞ≥Β | ≤Ϋ–– | ΙΪΫΜ≥Β | ΒΡ Ω | ΥΫΦ“≥Β |
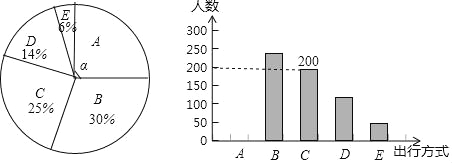
ΗυΨί“‘…œ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©≤Έ”κ±Ψ¥ΈΈ ΨμΒς≤ιΒΡ –ΟώΙ≤”– »ΥΘ§Τδ÷–―Γ‘ώBάύΒΡ»Υ ΐ”– »ΥΘΜ
Θ®2Θ©‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§«σAάύΕ‘”Π…»–Έ‘≤–ΡΫ«ΠΝΒΡΕ» ΐΘ§≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®3Θ©ΗΟ –‘Φ”–12Άρ»Υ≥ω––Θ§»τΫΪAΘ§BΘ§C’β»ΐάύ≥ω––ΖΫ ΫΨυ ”ΈΣΓΑ¬Χ…Ϊ≥ω––Γ±ΖΫ ΫΘ§«κΙάΦΤΗΟ –ΓΑ¬Χ…Ϊ≥ω––Γ±ΖΫ ΫΒΡ»Υ ΐΘ°