题目内容
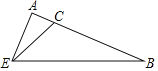
【题目】如图,矩形![]() 的顶点
的顶点![]() 在坐标原点,
在坐标原点,![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,当此矩形绕点
,当此矩形绕点![]() 旋转到如图
旋转到如图![]() 位置时
位置时![]() 的坐标为________.
的坐标为________.

【答案】![]()
【解析】
根据点B和点D的坐标得到OB=1,OD=![]() ,再根据旋转的性质得∠A′BC′=∠OBC=90°,OD=A′D′=BC′,利用等角的余角相等得到∠OBD=∠BC′H=∠CBC′,则可根据”AAS”判断△OBD≌△HC′B,则BH=OD=
,再根据旋转的性质得∠A′BC′=∠OBC=90°,OD=A′D′=BC′,利用等角的余角相等得到∠OBD=∠BC′H=∠CBC′,则可根据”AAS”判断△OBD≌△HC′B,则BH=OD=![]() ,C′H=OB=1,OH=OB+BH=1+
,C′H=OB=1,OH=OB+BH=1+![]() ,然后写出C′点的坐标.
,然后写出C′点的坐标.
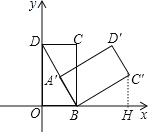
作C′H⊥x轴于H,如图,
∵点B的坐标为(1,0),点D的坐标为(0,3√),
∴OB=1,OD=![]() ,
,
∵矩形绕点B旋转到如图A′B′C′D′位置,
∴∠A′BC′=∠OBC=90°,OD=A′D′=BC′,
∠OBD=∠BC′H=∠CBC′,
在△OBD和△HC′B中,
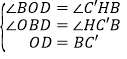 ,
,
∴△OBD≌△HC′B(AAS),
∴BH=OD=![]() ,C′H=OB=1,
,C′H=OB=1,
∴OH=OB+BH=1+![]() ,
,
∴C′点的坐标为(1+![]() ,1).
,1).
故答案为(1+![]() ,1).
,1).

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目