题目内容
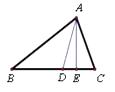
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,
,![]() 且
且![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图 1,求![]() 的度数;
的度数;
(2)如图 2,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)如图 3,在(2)的条件下,![]() 交
交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() ,
,![]() ,连接
,连接![]() ,若
,若![]() 的面积与
的面积与![]() 的面积差为 6,
的面积差为 6,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

【答案】(1)∠BFC=90°;(2)见解析;(3)![]() .
.
【解析】
(1)根据SAS证明![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)根据题意先求出![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() ,由
,由![]() ,
,![]() ,可证得
,可证得![]() ,
,![]() ,所以
,所以
![]() , 因为
, 因为![]() ,所以
,所以![]() .
.
(3)根据题意和(2)中结论先证明![]() ,过
,过 ![]() 作
作![]() 、
、![]() 垂线,垂足分别为
垂线,垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,证明
,证明![]() ,所以
,所以![]() ,然后根据等腰三角形的性质可得出
,然后根据等腰三角形的性质可得出![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,所以
,所以![]() ,设
,设![]() ,
,![]() ,
,
所以![]()
![]()
![]() ,
,![]() ,求出x,y,不难得到
,求出x,y,不难得到![]() =
=![]() ,然后可得
,然后可得![]() .
.
(1)因为![]() 是等腰直角三角形,所以
是等腰直角三角形,所以![]() ,
,![]() , 所以
, 所以![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.

(2)因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
由(1)知:![]() ,所以
,所以![]() ,
,
设![]() , 所以
, 所以![]() ,所以
,所以![]() ,
,
所以![]() , 因为
, 因为![]() 平分
平分![]() ,所以
,所以![]() ,
,
在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() , 因为
, 因为![]() ,所以
,所以![]() .
.

(3)由(2)知:![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
过 ![]() 作
作![]() 、
、![]() 垂线,垂足分别为
垂线,垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 平分
平分![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
设![]() ,所以
,所以![]() ,设
,设![]() ,所以
,所以![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]()
![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以![]() .
.


练习册系列答案
相关题目
【题目】为了创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶,![]() ,
,![]() ,
,![]() 三个小区所购买的数量和总价如表所示.
三个小区所购买的数量和总价如表所示.
甲型垃圾桶数量(套) | 乙型垃圾桶数量(套) | 总价(元) | |
|
|
|
|
|
|
|
|
|
|
|
|
(1)问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元?
(2)求![]() ,
,![]() 的值.
的值.