题目内容
【题目】如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B,∠B=2∠DAE,那么∠ACB的度数为.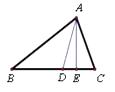
【答案】72°
【解析】∵AE是高,
∴∠AED=∠AEC=90°,
又∵AD是角平分线,
∴∠BAD=∠CAD=![]() ∠BAC,
∠BAC,
∴∠DAE=∠DAC-∠CAE=![]() ∠BAC-(90°-∠ACB),
∠BAC-(90°-∠ACB),
又∵∠BAC=2∠B,
∴∠BAC+∠B+∠ACB=180°,
∴∠ACB=180°-3∠B,
又∵∠B=2∠DAE,
∴∠DAE=![]() ∠B,
∠B,
∴![]() ∠B=
∠B=![]() ×2∠B-【90°-(180°-3∠B)】,
×2∠B-【90°-(180°-3∠B)】,
∴∠B=36°,
∴∠ACB=180°-3×36°=72°,
所以答案是:72°.
【考点精析】根据题目的已知条件,利用角的平分线和三角形的内角和外角的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目