题目内容
【题目】如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD长( )
A.4 ![]() cm
cm
B.3 ![]() cm
cm
C.5 ![]() cm
cm
D.4 cm
【答案】A
【解析】连接BC,BD,OD,且OD交BC于点E,
∵AB为直径,
∴∠ADB=∠ACB=90°,
又∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴弧CD=弧BD,
∴OD垂直平分BC,
即E为BC中点,
在Rt△ACB中,
∵AB=10cm,AC=6cm,
∴BC=![]() =8cm,
=8cm,
∴OE=![]() AC=3,BE=
AC=3,BE=![]() BC=4,
BC=4,
∴DE=OD-OE=5-3=2,
∴在Rt△BDE中,BD=![]() =2
=2![]() ,
,
∴在Rt△ADB中,AD=![]() =4
=4![]() ,
,
故答案为:A.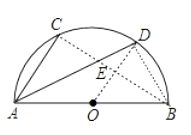
连接BC,BD,OD,且OD交BC于点E,根据直径所对的圆周角为90°得出∠ADB=∠ACB=90°,由AD平分∠BAC得出∠CAD=∠BAD,由圆周角定理得出弧CD=弧BD,再根据垂径定理得出OD垂直平分BC;在Rt△ACB中,由勾股定理得出BC=8cm,从而求出OE=3,BE=4,DE=2,在Rt△BDE和在Rt△ADB中,由勾股定理分别求出BD=2![]() ,AD=4
,AD=4![]() .
.

练习册系列答案
相关题目
【题目】某校抽样调查了七年级学生每天体育锻炼时间,整理数据后制成了如下所示的频数分布表,这个样本的中位数在第 组.
组别 | 时间(小时) | 频数(人) |
第1组 | 0≤t<0.5 | 12 |
第2组 | 0.5≤t<1 | 24 |
第3组 | 1≤t<1.5 | 18 |
第4组 | 1.5≤t<2 | 10 |
第5组 | 2≤t<2.5 | 6 |