题目内容
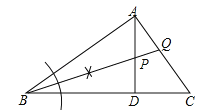
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠ABC的平分线分别交AD,AC于P,Q两点,证明:AP=AQ.

【答案】(1)(2)见解析
【解析】试题分析:(1)作出角平分线BQ即可.
(2)根据余角的定义得出∠AQP+∠ABQ=90°,根据角平分线的性质得出∠ABQ=∠PBD,再由∠BPD=∠APQ可知∠APQ=∠AQP,据此可得出结论.
试题解析:解:(1)BQ就是所求的∠ABC的平分线,P、Q就是所求作的点.
(2)证明:∵AD⊥BC,∴∠ADB=90°,∴∠BPD+∠PBD=90°.
∵∠BAC=90°,∴∠AQP+∠ABQ=90°.
∵∠ABQ=∠PBD,∴∠BPD=∠AQP.
∵∠BPD=∠APQ,∴∠APQ=∠AQP,∴AP=AQ.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目