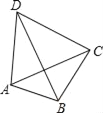
[题目]如图.四边形ABCD的对角线AC与BD互相垂直.若AB=3.BC=4.CD=5.则AD的长为( )A. 3 B. 4 C. 2 D. 4 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，四边形ABCD的对角线AC与BD互相垂直，若AB=3，BC=4，CD=5，则AD的长为（　　）

A. 3 B. 4 C. 2 D. 4

【答案】A

【解析】

根据勾股定理可得，在Rt△AOB中AO2=AB2-BO2；在Rt△DOC中可得DO2=DC2-CO2；在Rt△BOC中可得BC2=OB2+CO2；即可得AD2=AO2+DO2=AB2-BO2+DC2-CO2= AB2 +DC2-（CO2+BO2），代入数值计算后，即可求得 AD的长.

如图，在Rt△AOB中可得，AO2=AB2-BO2；

在Rt△DOC中可得：DO2=DC2-CO2；

在Rt△BOC中可得：BC2=OB2+CO2；

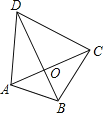
∴AD2=AO2+DO2=AB2-BO2+DC2-CO2= AB2 +DC2-（CO2+BO2）=32+52-42=18，

∴AD= ．

故选A．

练习册系列答案

解：如图①，过点E作EF∥AB

∴∠BAE＝∠1（　　）

∵AB∥CD（　　）

∴CD∥EF（　　）

∴∠2＝∠DCE

∴∠BAE+∠DCE＝∠1+∠2（　　）

∴∠BAE+∠DCE＝∠AEC

（探究）当点E在如图②的位置时，其他条件不变，试说明∠AEC+∠FGC+∠DCE＝360°；

（应用）点E、F、G在直线AB与CD之间，连结AE、EF、FG和CG，其他条件不变，如图③．若∠EFG＝36°，则∠BAE+∠AEF+∠FGC+∠DCG＝　　°．

【题目】如图，对正方形纸片ABCD进行如下操作：
（i）过点D任作一条直线与BC边相交于点E1（如图①），记∠CDE1=α1；
（ii）作∠ADE1的平分线交AB边于点E2（如图②），记∠ADE2=α2；
（iii）作∠CDE2的平分线交BC边于点E3（如图③），记∠CDE3=α3；
按此作法从操作（2）起重复以上步骤，得到α1 ， α2 ， …，αn ， …，现有如下结论：①当α1=10°时，α2=40°；②2α4+α3=90°； ③当α5=30°时，△CDE9≌△ADE10；④当α1=45°时，BE2= ．
其中正确的个数为（）
A.1
B.2
C.3
D.4

【题目】如图，△ABC中，∠BAC=90°，AD⊥BC，垂足为D．

（1）求作∠ABC的平分线（要求：尺规作图，保留作图痕迹，不写作法）；

（2）若∠ABC的平分线分别交AD，AC于P，Q两点，证明：AP=AQ．

【题目】如图，四边形ABCD是边长为a的正方形，点G、E分别是边AB、BC的中点，∠AEF=90°，且EF交正方形外角的平方线CF于点F．
（1）证明：△AGE≌△ECF；
（2）求△AEF的面积．

【题目】如图所示，(1)∠BED与∠CBE是直线________，________被直线________所截形成的________角；

(2)∠A与∠CED是直线________，________被直线________所截形成的________角；

(3)∠CBE与∠BEC是直线________，________被直线________所截形成的________角；

(4)∠AEB与∠CBE是直线________，________被直线________所截形成的________角．

【题目】如图，在平面直角坐标系上，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，点B（1，3），将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE，恰好有一反比例函数y= 图像恰好过点D，则k的值为（）

A.6
B.﹣6
C.9
D.﹣9

【题目】生活经验表明，靠墙摆放梯子时，若梯子底端离墙的距离约为梯子长度的，则梯子比较稳定，如图，AB为一长度为6米的梯子．

（1）当梯子稳定摆放时，它的顶端能达到5.7米高的墙头吗？

（2）如图2，若梯子底端向左滑动（3﹣2）米，那么梯子顶端将下滑多少米？

【题目】在△AOB中，∠AOB=90°，AO=6厘米，BO=8厘米，分别以OB和OA所在直线为x轴，y轴建立平面直角坐标系，如图所示，动点M从点A开始沿AO方向以2厘米/秒的速度向点O移动，同时动点N从点O开始沿OB方向以4厘米/秒的速度向点B移动（其中一点到达终点时，另一点随即停止移动）．

（1）求过点A和点B的直线表达式；
（2）当点M移动多长时间时，四边形AMNB的面积最小？并求出四边形AMNB面积的最小值；
（3）在点M和点N移动的过程中，是否存在以O，M，N为顶点的三角形与△AOB相似？若存在，请求出点M 和点N的坐标；若不存在，请说明理由．

试题分类