题目内容
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( ) 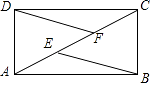
A.![]()
B.1
C.![]()
D.![]()
【答案】D
【解析】解:∵矩形ABCD中,AB=4,AD=2, ∴AB∥CD,AB=CD,∠BAD=∠ABC=90°,矩形ABCD的面积=4×2=8,
∴∠DCF=∠BAE,
在△DCF和△BAE中, 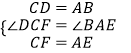 ,
,
∴△DCF≌△BAE(SAS),
∴DF=BE,∠DFC=∠BEA,
∴∠DFE=∠BEF,
∴DF∥BE,
∵AE=EF=FC,
∴△BCE的面积= ![]() ×8=
×8= ![]() ,
,
延长BE交AD于G,延长DF交BC于H,作FM⊥BE于M,CN⊥BE于N,则FM∥CN,
∵AE=EF=FC,
∴AG=DG=1,BH=CH=1,
∴BG= ![]() =
= ![]() ,
,
∴BE= ![]() BG=
BG= ![]() ,
,
∵ ![]() BECN=
BECN= ![]() ,
,
∴CN= ![]() ,
,
∵FM∥CN,EF=FC,
∴FM= ![]() CN=
CN= ![]() ,
,
故选:D.
【考点精析】关于本题考查的矩形的性质,需要了解矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目