题目内容
【题目】如图，直线y=x+3分别交x，y轴于点D，C，点B在x轴上，OB=OC，过点B作直线m∥CD．点P、Q分别为直线m和直线CD上的动点，且点P在x轴的上方，满足∠POQ=45°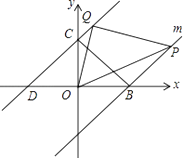
（1）则∠PBO=度；
（2）问：PBCQ的值是否为定值？如果是，请求出该定值；如果不是，请说明理由；
（3）求证：CQ2+PB2=PQ2 ．
【答案】
（1）135
（2）
解：PBCQ是定值，理由如下：
∠OCQ=∠ODC+∠COD=45°+90°=135°=∠PBO，
∵∠COQ+∠CQO=180°﹣∠OCQ=45°，∠BOP+∠BPO=180°﹣∠PBO=45°，
∴∠COQ+∠CQO=∠BOP+∠BPO=45°，
又∵∠COQ+∠BOP=∠BOC﹣∠POQ=90°﹣45°=45°，
∴∠COQ=∠BPO，∠CQO=∠BOP，
∴△COQ∽△BPO，
∴ 
，即PBCQ=OBOC=9
（3）
解：证明：过点Q作QE⊥m于点E，如图1所示．
∵OB=OC=3，∠BOC=90°，
∴∠OBC=45°，BC=3 
．
∴∠PBC=∠PBO﹣∠OBC=135°﹣45°=90°，
又∵QE⊥m，
∴CB∥QE，∠PEQ=90°．
∵直线m∥直线CD，
∴四边形BEQC为矩形，
∴QE=CB=3 ．
在Rt△QEP中，∠PEQ=90°，PE=PB﹣CQ，QE=3 ，
∴PQ2=QE2+PE2=18+（PB﹣CQ）2，
又∵PBCQ=9，
∴PQ2=2PBCQ+（PB﹣CQ）2=PB2+CQ2
【解析】解：（1）令x=0，则y=3，
即点C的坐标为（0，3）；
令y=0，则有x+3=0，
解得：x=﹣3，即点D的坐标为（﹣3，0）．
又∵OB=OC，
∴OC=OD=OB=3．
∵tan∠ODC= 
=1，
∴∠ODC=45°，
∵直线m∥直线CD，
∴∠ODC+∠PBO=180°，
∴∠PBO=135°．
所以答案是：135
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．
