题目内容
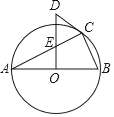
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
【答案】(1)证明见解析;(2)∠CDE=2∠A,理由见解析.
【解析】分析:(1)由勾股定理求AB,证明△AOE∽△ACB,根据相似三角形的对应线段成比例求OE;(2)连接OC,可知∠3=2∠A,只需用同角的余角证∠D=∠3即可.
详解:(1)∵AB为⊙O的直径,∴∠ACB=900,
在Rt△ABC中,由勾股定理得:AB=![]() =3
=3![]() ,
,
∴OA=![]() AB=
AB=![]() .
.
∵OD⊥AB,∴∠AOE=∠ACB=900,由∵∠A=∠A,∴△AOE∽△ACB,
∴![]() ,即
,即![]() ,解得:OE=
,解得:OE=![]() .
.
(2)∠CDE=2∠A,
理由如下:连接OC,如图所示:
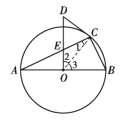
∵OA=OC,∴∠1=∠A,
∵CD是⊙O的切线,∴OC⊥CD,∴∠OCD=900,∴∠2+∠CDE=900,
∵OD⊥AB,∴∠2+∠3=900,∴∠3=∠CDE,∵∠3=∠A+∠1=2∠A,
∴∠CDE=2∠A.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目