题目内容
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的解析式;
(2)如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(3)如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
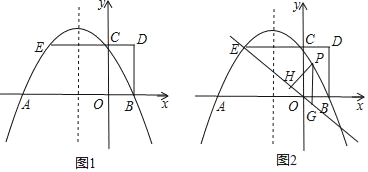
【答案】(1)抛物线解析式为y=﹣![]() x2﹣
x2﹣![]() x+2;(2)l=﹣
x+2;(2)l=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,![]() ;(3)(2,﹣
;(3)(2,﹣![]() )或(﹣4,﹣
)或(﹣4,﹣![]() )或(﹣2,2).
)或(﹣2,2).
【解析】试题分析:(1)由条件可求得A、B的坐标,利用待定系数法可求得抛物线解析式;
(2)可先求得E点坐标,从而可求得直线OE解析式,可知∠PGH=45°,用m可表示出PG的长,从而可表示出l的长,再利用二次函数的性质可求得其最大值;
(3)分AC为边和AC为对角线,当AC为边时,过M作对称轴的垂线,垂足为F,则可证得△MFN≌△AOC,可求得M到对称轴的距离,从而可求得M点的横坐标,可求得M点的坐标;当AC为对角线时,设AC的中点为K,可求得K的横坐标,从而可求得M的横坐标,代入抛物线解析式可求得M点坐标.
试题解析:(1)∵矩形OBDC的边CD=1,∴OB=1,∵AB=4,∴OA=3,∴A(﹣3,0),B(1,0),把A、B两点坐标代入抛物线解析式可得:![]() ,解得:
,解得: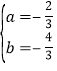 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)在![]() 中,令y=2可得2=
中,令y=2可得2=![]() ,解得x=0或x=﹣2,∴E(﹣2,2),∴直线OE解析式为y=﹣x,由题意可得P(m,
,解得x=0或x=﹣2,∴E(﹣2,2),∴直线OE解析式为y=﹣x,由题意可得P(m,![]() ),∵PG∥y轴,∴G(m,﹣m),∵P在直线OE的上方,∴PG=
),∵PG∥y轴,∴G(m,﹣m),∵P在直线OE的上方,∴PG=![]() ﹣(﹣m)=
﹣(﹣m)=![]() =
=![]() ,∵直线OE解析式为y=﹣x,∴∠PGH=∠COE=45°,∴l=
,∵直线OE解析式为y=﹣x,∴∠PGH=∠COE=45°,∴l=![]() PG=
PG=![]() [
[![]() ]=
]=![]() ,∴当m=
,∴当m=![]() 时,l有最大值,最大值为
时,l有最大值,最大值为![]() ;
;
(3)①当AC为平行四边形的边时,则有MN∥AC,且MN=AC,如图,过M作对称轴的垂线,垂足为F,设AC交对称轴于点L,则∠ALF=∠ACO=∠FNM,在△MFN和△AOC中,∵∠MFN=∠AOC,∠FNM=∠ACO,MN=AC,∴△MFN≌△AOC(AAS),∴MF=AO=3,∴点M到对称轴的距离为3,又![]() ,∴抛物线对称轴为x=﹣1,设M点坐标为(x,y),则|x+1|=3,解得x=2或x=﹣4,当x=2时,y=﹣
,∴抛物线对称轴为x=﹣1,设M点坐标为(x,y),则|x+1|=3,解得x=2或x=﹣4,当x=2时,y=﹣![]() ,当x=﹣4时,y=
,当x=﹣4时,y=![]() ,∴M点坐标为(2,﹣
,∴M点坐标为(2,﹣![]() )或(﹣4,﹣
)或(﹣4,﹣![]() );
);
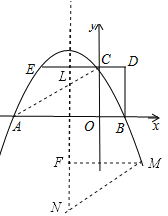
②当AC为对角线时,设AC的中点为K,∵A(﹣3,0),C(0,2),∴K(﹣![]() ,1),∵点N在对称轴上,∴点N的横坐标为﹣1,设M点横坐标为x,∴x+(﹣1)=2×(﹣
,1),∵点N在对称轴上,∴点N的横坐标为﹣1,设M点横坐标为x,∴x+(﹣1)=2×(﹣![]() )=﹣3,解得x=﹣2,此时y=2,∴M(﹣2,2);
)=﹣3,解得x=﹣2,此时y=2,∴M(﹣2,2);
综上可知点M的坐标为(2,﹣![]() )或(﹣4,﹣
)或(﹣4,﹣![]() )或(﹣2,2).
)或(﹣2,2).

 名校课堂系列答案
名校课堂系列答案【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?