题目内容
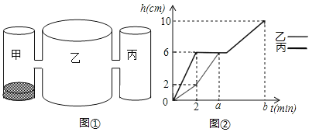
【题目】实验室里，水平桌面上有甲、乙、丙三个高都是10cm的圆柱形容器（甲、丙的底面积相同），用两个相同的管子在容器的6cm高度处连通（即管子底离容器底6
，管子的体积忽略不计），、现在三个容器中，只有甲中有水，水位高2，如图①所示，若每分钟同时向乙、丙中注入相同量的水，到三个容器都注满水停止，乙、丙容器中的水位
（）与注水时间
（
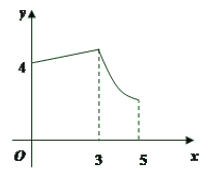
）的图象如图②所示．
（1）乙、丙两个容器的底面积之比为 ．
（2）图②中
的值为 ，
的值为 ．
（3）注水多少分钟后，乙与甲的水位相差2？
【答案】（1）3：1；（2）4；8；（3）注水3分钟或4
分钟
【解析】
（1）观察图象即可解决问题；
（2）根据（1）的结论，结合图象解答即可；
（3）分情况解答：①当乙容器的水位达到4cm时；②当甲容器的水位达到4cm时．
(1)由图②可知：注水2分钟时，乙的水位高2cm，丙的水位高为6cm
∵每分钟同时向乙、丙容器中注入相同量的水
∴根据圆柱的体积公式可得：
S乙×2=S丙×6，
∴S乙：S丙=3：1，
∴乙、丙两容器的底面积之比为3：1．
故答案为3：1；
(2)由(1)可知：根据圆柱的体积公式可得：
S丙×3=3S丙，
∴每分钟向丙注水量为3S丙，
到乙、丙容器内的水的高度都为6cm时，乙需要的水量为：S乙×6=3S丙×6=18S丙，
丙需要的水量为S丙 ×6=6S丙
∴a×2x3S丙=18S丙+6S丙，
∴a=4，
到三个容器注满水时，甲需要的水量为：S丙×(10-2)=8S丙，
到三个容器注满水时，乙需要的水量为：S乙×10=3S丙×10=30S丙，
到三个容器注满水时，丙需要的水量为：S丙×10=10S丙
∵每分钟向乙、丙注水量都为：3S丙，
∴b×2×3S丙=8S丙+30S丙+10S丙
∴b=8
故答案为4；8；
(3)当2≤x≤4时，设乙容器水位高度h与时间t的函数关系式为h=kt+b(k=0)，
．图象经过(2，2)、(4，6)两点，
∴
解得
·
∴．h=2t-2(2≤t≤t)
当甲容器水位高2cm，乙容器水位高4cm时，乙比甲的水位高2cm，
令h=4，即4=2t-2，
解得t=3；
当甲容器水位高4cm，乙容器水位高6cm时，乙比甲的水位高2cm，
t=4+
．
综上所述，注水3分钟或4分钟时，乙比甲的水位高2cm．
