Question

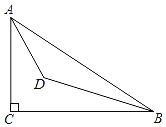
【题目】如图，△ABC中，AC＝4，BC＝3，AB＝5，AD为△ABC的角平分线，则CD的长度为（　　）

A.1B.C.D.

Answer 1

【答案】D

【解析】

过D作DP⊥AP于P，根据角平分线的性质可知∠CAD=∠BAD，利用AAS定理可知△ACD≌△APD.在在Rt△ABC中根据勾股定理得出AB的长，设DP=x，则DP=x，BD=3-x，在Rt△DPB中，利用勾股定理即可得出结论.

解：∵AC＝4，BC＝3，AB＝5，

∴BC2+AC2＝32+42＝52＝AB2，

∴∠C＝90°，

过D作DP⊥AP于P，

∵AD平分∠BAC，

∴∠CAD＝∠BAD．

又∵DC⊥AC、DP⊥AB，

∴∠C＝∠APD．

在△ACD与APD中，

∵

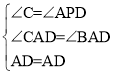
∴△ACD≌APD（AAS），

∴AP＝AC＝4，CD＝PD，

设DP=x，则CP＝x，BD＝3﹣x，

在Rt△DPB中，∠DPB＝90°，

∴DP2+PB2＝DB2，

即x2+12＝（3﹣x）2，

解得

∴

故选：D．