Question

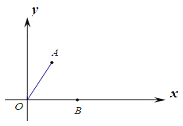
【题目】如图，在平面直角坐标系中，A（1，），B（2，0），C点在x轴上运动，过点Ｏ作直线ＡC的垂线，垂足为D.当点C在x轴上运动时，点D也随之运动．则线段BD长的最大值为______________．

Answer 1

【答案】+1

【解析】根据圆周角定理的推论可得出点D在以AO中点E为圆心，AO为直径的圆上，连接BE并延长交圆E于点D，此时BD最长，利用等边三角形的性质即可求出BD的最大值.

∵ＯE垂直于直线ＡC，垂足为D，

作AO的中点E，

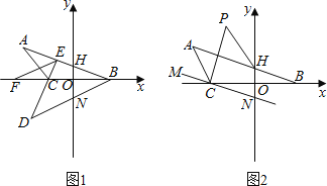
∴点D在以E为圆心，AO长为直径的圆上（如图1所示），

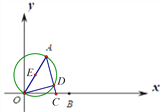
图1

连接BE并延长交圆E于点D，此时BD最长（如图2所示），

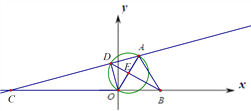
图2

连接AB，,

∵A（1，），

∴且，

∴,

∵B（2，0），

∴OB=2,

∴为等边三角形，

∵E是AO的中点，

∴ED＝OE＝AO＝1，

∴BE＝

∴BD＝BE+ED=+1.

故答案为：+1.