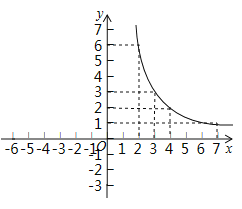题目内容
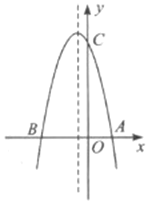
【题目】二次函数y＝x2﹣6x+m满足以下条件：当﹣2＜x＜﹣1时，它的图象位于x轴的下方；当8＜x＜9时，它的图象位于x轴的上方，则m的值为（ ）
A.27B.9C.﹣7D.﹣16
【答案】D
【解析】
先确定抛物线的对称轴为直线x＝3，根据抛物线的对称性得到x＝2和x＝8时，函数值相等，然后根据题意判断抛物线与x轴的交点坐标为（2，0），（8，0），最后把（2，0）代入y＝x26x＋m可求得m的值．
解：∵抛物线的对称轴为直线x＝
，
∴x＝2和x＝8时，函数值相等，
∵当2＜x＜1时，它的图象位于x轴的下方；当8＜x＜9时，它的图象位于x轴的上方，
∴抛物线与x轴的交点坐标为（2，0），（8，0），把（2，0）代入y＝x26x＋m得4＋12＋m＝0，解得m＝16．
故选：D．
【题目】第二十届冬季奥林匹克运动会将于2022年在北京市和张家口市举行，为了调查学生对冬季奥运会知识的了解情况，某校对七、八年级全体学生进行了相关知识的测试，然后从七、八年级各抽20名学生的成绩（百分制），并对数据进行了整理、描述和分析，给出了部分信息．
1.七年级20名学生成绩的频数分别如下：
成绩m分 | 频数（人数） |
| 1 |
| 2 |
| 3 |
| 8 |
| 6 |
合计 | 20 |
2.七年级20名学生成绩在
这一组的具体成绩是：
87，88，88，88，89，89，89，89
3.七、八年级学生样本成绩的平均数，中位数，众数如下表所示：
平均数 | 中位数 | 众数 | |
七年级 | 84 | n | 89 |
八年级 | 84.2 | 85 | 85 |
根据以上信息，解得下列问题：
（1）表中n的值是 ．
（2）在学生样本成绩中，某学生的成绩是87分，在他所述的年级抽取的学生中排在前10名，根据表中数据判断该生所在年级，并说明理由；
（3）七年级共有180名学生，若将不低于80分的成绩定为优秀学生，请估计七年级成绩优秀的人数．
【题目】小楠是一个乐学习，善思考，爱探究的同学，她对函数
的图象和性质进行了探究，请你将下列探究过程补充完整：
（1）函数的自变量
的取值范围是________________；
（2）用描点法画函数图象：
①列表：
| … | -5 | -2 | -1 | 0 | … | 2 | 3 | 4 | 7 | … |
| … |
| 2 | 3 |
| … | 6 | 3 | 2 | 1 | … |
表中
的值为______________，
的值为_______________．
②描点连线：请在右图画出该图象的另一部分．
（3）观察函数图象，得到函数的性质之一：当_____________时，函数值
随的增大而增大．
（4）应用：若
，则的取值范围是______________．
