题目内容
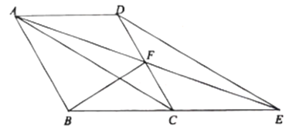
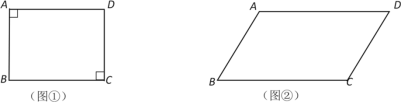
【题目】(1)如图①,在四边形ABCD中,∠A=∠C=90°,AB=CD,求证:四边形ABCD是矩形;
(2)如图②,若四边形ABCD满足∠A=∠C>90°,AB=CD,求证:四边形ABCD是平行四边形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)连接BD,证明Rt△ABD≌Rt△CDB得AD=CB,根据两组对边分别相等的四边形是平行四边形可证明四边形ABCD是平行四边形,再根据有一个是直角的平行四边形是矩形可得结论;
(2)分别过点B、D作BE⊥AD于点E,DF⊥BC于点F,证明△ABE≌△CDF,进而证明四边形EBFD是矩形,再根据两组对边分别相等的四边形是平行四边形即可得到结论.
(1)证明:如图①,连接BD,
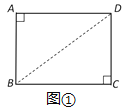
∵∠A=∠C=90°,在Rt△ABD和Rt△CDB中,
AB=CD,BD=DB,
∴Rt△ABD≌Rt△CDB(HL).
∴AD=CB,
∴四边形ABCD是平行四边形,
∵∠A=90°,
∴四边形ABCD是矩形.
(2)如图②,分别过点B、D作BE⊥AD于点E,DF⊥BC于点F,
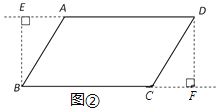
∵∠BAD=∠BCD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,∠AEB=∠CFD=90°,∠BAE=∠DCF,AB=CD,
∴△ABE≌△CDF(AAS),
∴BE=DF,AE=CF,
由(1)可得四边形EBFD是矩形,
∴ED=BF,
∴AD=BC,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】第二十届冬季奥林匹克运动会将于2022年在北京市和张家口市举行,为了调查学生对冬季奥运会知识的了解情况,某校对七、八年级全体学生进行了相关知识的测试,然后从七、八年级各抽20名学生的成绩(百分制),并对数据进行了整理、描述和分析,给出了部分信息.
1.七年级20名学生成绩的频数分别如下:
成绩m分 | 频数(人数) |
| 1 |
| 2 |
| 3 |
| 8 |
| 6 |
合计 | 20 |
2.七年级20名学生成绩在![]() 这一组的具体成绩是:
这一组的具体成绩是:
87,88,88,88,89,89,89,89
3.七、八年级学生样本成绩的平均数,中位数,众数如下表所示:
平均数 | 中位数 | 众数 | |
七年级 | 84 | n | 89 |
八年级 | 84.2 | 85 | 85 |
根据以上信息,解得下列问题:
(1)表中n的值是 .
(2)在学生样本成绩中,某学生的成绩是87分,在他所述的年级抽取的学生中排在前10名,根据表中数据判断该生所在年级,并说明理由;
(3)七年级共有180名学生,若将不低于80分的成绩定为优秀学生,请估计七年级成绩优秀的人数.