题目内容
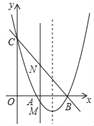
【题目】如图，二次函数
的图像交
轴于
，交
轴于
，过
画直线。
（1）求二次函数的解析式；
（2）点
在轴正半轴上，且
，求
的长；
（3）点
在二次函数图像上，以为圆心的圆与直线
相切，切点为
。
① 点在轴右侧，且
（点
与点
对应），求点的坐标；
② 若
的半径为
，求点的坐标。
【答案】（1）
（2）3/2（3）①
或
②
或
【解析】
解：（1）∵二次函数
的图像交
轴于
∴设该二次函数的解析式为：
………………1分
又二次函数的图像交
轴于
将
代入，得
解得，
………………2分
∴抛物线的解析式为
，即………………3分
（2）设
，则
在
中，
由勾股定理，得
………………4分
解得，
，即
………………5分
（3）① ∵
，点
与点
对应
∴
情形1：如图，当
在点下方时
∵
∴
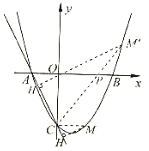
轴，∴
点
在二次函数图像上
∴
………………6分
解得
（舍去）或
，∴
………………7分
情形2：如图，当在点上方时
∵
由（2）得，
为直线
与抛物线的另一交点
设直线
的解析式为
把
的坐标代入，得
解得，
，∴
………………8分
由
，解得，（舍去）或
此时
，∴
………………9分
∴点的坐标为或
②以为圆心的圆与直线
相切，则点到直线的距离即为圆半径
。因为同时也在抛物线上，因此利用平行线间距离处处相等的性质，先在轴上找到与直线距离为的点
，过点作与直线平行的直线，根据平行直线的解析式中
相等的性质确定直线解析式，再联立直线与抛物线解析式求得坐标。
在轴上取一点，过点作
于点
，使
∵
∴
，∴
∴
，解得
∴
或
过点作
，交抛物线于点
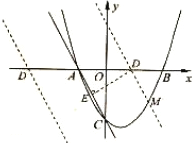
设直线的解析式为，将
代入可得，
，解得
∴设直线
的解析式为
，将或代入可得，
或
，解得
或
则直线的解析式为
或
当
时，
，
，方程无实数解 ………………10分
当
时，
，
解得
∴点坐标为或……………12分
练习册系列答案
相关题目
