题目内容
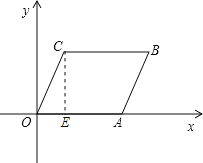
【题目】如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴上;∠COA=∠B=60°,且CB∥OA.
(1)求证,四边形OABC是平行四边形.
(2)若A的坐标为(8,0),OC长为6,求点B的坐标.

【答案】(1)见解析 (2)B(11,3![]() )
)
【解析】
(1)根据平行线的性质求得∠OAB=180°﹣∠B=120°,则同旁内角∠COA+∠OAB=180°,易证OC∥AB,所以“有两组对边相互平行的四边形是平行四边形”.
(2)过点C作CE⊥OA于点E,通过解直角△COE可以确定OE、CE的长度,则由平行四边形的性质不难求得B点坐标.
(1)证明:如图,∵CB∥OA,∠B=60°,
∴∠OAB=180°﹣∠B=120°,
又∵∠COA=60°,
∴∠COA+∠OAB=180°,
∴OC∥AB,
∴四边形OABC是平行四边形.
(2)解:如图,过点C作CE⊥OA于点E.
∵∠B=60°,OC长为6,
∴OE=OCcos60°=3,CE=OCsin60°=3![]() .则C(3,3
.则C(3,3![]() ).
).
∵BC∥OA,BC=OA=8,
∴B(11,3![]() ).
).

练习册系列答案
相关题目






