Question

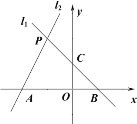
【题目】如图，ΔABC中，∠ABC与∠ACB的平分线交于点I，根据下列条件，求∠BIC的度数。

①若∠ABC＝40°，∠ACB＝60°，则∠BIC＝______°；

②若∠ABC＋∠ACB＝100°，则∠BIC=___________°；

③若∠A＝80°，则∠BIC＝_______°；

④从上述计算中，我们能发现已知∠A=x，则∠BIC＝_______°.

Answer 1

【答案】①130；②130；③130；④90°+．

【解析】

①由∠ABC=40°，∠ACB=60°，∠ABC与∠ACB的平分线交于点I，可求∠IBC、∠ICB的度数，再利用三角形内角和定理求∠BIC；

②由∠ABC+∠ACB=100°，∠ABC与∠ACB的平分线交于点I，可求∠IBC+∠ICB的度数，再利用三角形内角和定理求∠BIC；

③由∠A=80°可得∠ABC+∠ACB=100°，∠ABC与∠ACB的平分线交于点I，可求∠IBC+∠ICB的度数，再利用三角形内角和定理求∠BIC；

④由三角形内角和定理得∠ABC+∠ACB=180°﹣∠A，∠ABC与∠ACB的平分线交于点I，则∠IBC+∠ICB（180°﹣∠A）．在△IBC中，利用三角形内角和定理求∠BIC．

①∵∠ABC=40°，∠ACB=60°，∠ABC与∠ACB的平分线交于点I，∴∠IBC=20°∠ICB=30°，∴∠BIC=180°﹣∠IBC﹣∠ICB=130°；

②∵∠ABC+∠ACB=100°，∠ABC与∠ACB的平分线交于点I，∴∠IBC+∠ICB（∠ABC+∠ACB）=50°，∴∠BIC=180°﹣（∠IBC+∠ICB）=130°；

③∵∠A=80°，∴∠ABC+∠ACB=100°．

又∵∠ABC与∠ACB的平分线交于点I，∴∠IBC+∠ICB（∠ABC+∠ACB）=50°，∴∠BIC=180°﹣（∠IBC+∠ICB）=130°；

④∠BIC=90°x．理由如下：

在△ABC中，∠ABC+∠ACB=180°﹣∠A．

∵BI、CI是△ABC内角的平分线，∴∠IBC∠ABC，∠ICB∠ACB，∴∠IBC+∠ICB∠ABC∠ACB（∠ABC+∠ACB）（180°﹣∠A）．

在△IBC中，∠BIC=180°﹣（∠IBC+∠ICB）=180°（180°﹣∠A）=90°∠A．

即：∠BIC=90°x．