��Ŀ����
����Ŀ����������ABCD�У�����E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ�.
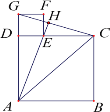
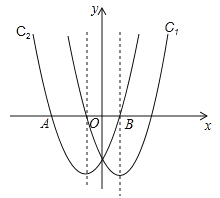
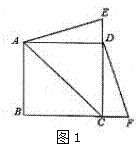
��1����ͼ1������E�ڱ�DC����D��C�ƶ���ͬʱ��F�ڱ�CB����C��B�ƶ�ʱ������AE��DF���ڵ�P������д��AE��DF��������ϵ��λ�ù�ϵ����˵������
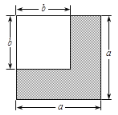
��2����ͼ2����E��F�ֱ��ڱ�CD��BC���ӳ������ƶ�ʱ������AE��DF����1���еĽ��ۻ������𣿣�����ֱ�ӻش���������������������֤����������AC������ACEΪ����������ʱCE��CD��ֵ��
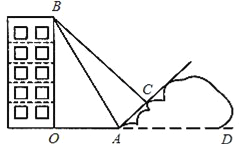
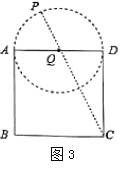
��3����ͼ3����E��F�ֱ���ֱ��DC��CB���ƶ�ʱ������AE��DF���ڵ�P�����ڵ�E��F���ƶ���ʹ�õ�PҲ��֮�˶������㻭����P�˶�·���IJ�ͼ.��AD=2��������߶�CP�����ֵ.

ͼ1 ͼ2 ͼ3
���𰸡���1��AE=DF��AE��DF�����ɼ���������2��������CE:CD=![]() ��2����3��
��2����3�� ![]()
�������������������1�����������ε����ʣ���SAS��֤����ADE�ա�DCF����ȫ�������ε����ʵ�AE=DF����DAE=��CDF�����ɵȽǵ������ȿɵ�AE��DF��
��2��������������ٵ�AC=CEʱ����������ABCD�ı߳�Ϊa���ɹ��ɶ������AC=CE=![]() a���ɣ��ڵ�AE=ACʱ���������εı߳�Ϊa���ɹ��ɶ������AC=AE=
a���ɣ��ڵ�AE=ACʱ���������εı߳�Ϊa���ɹ��ɶ������AC=AE=![]() a�����������ε�����֪��ADC=90�㣬Ȼ����ݵ��������ε����ʵó�DE=CD=a���ɣ�
a�����������ε�����֪��ADC=90�㣬Ȼ����ݵ��������ε����ʵó�DE=CD=a���ɣ�
��3���ɣ�1����2��֪����P��·����һ����ADΪֱ����Բ����AD���е�ΪQ������QC�����ڵ�P����ʱCP�ij���������ɹ��ɶ����ɵ�QC�ij�������CP���ɣ�
�����������1��AE=DF��AE��DF��
�����ǣ����ı���ABCD�������Σ�
��AD=DC����ADE=��DCF=90����
�߶���E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ���
��DE=CF��
����ADE����DCF��
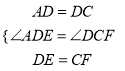 ��
��
��![]() ��
��
��AE=DF����DAE=��FDC��
�ߡ�ADE=90�������ADP+��CDF=90����
���ADP+��DAE=90����
���APD=180��-90��=90����
��AE��DF��
��2����1���еĽ��ۻ�������
�����������
����ͼ1����AC=CEʱ��
��������ABCD�ı߳�Ϊa���ɹ��ɶ����ã�
![]() ��
��
��![]() ��
��
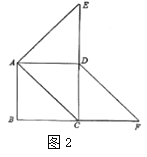
����ͼ2����AE=ACʱ��
��������ABCD�ı߳�Ϊa���ɹ��ɶ����ã�
![]() ��
��
���ı���ABCD�������Σ�
���ADC=90������AD��CE��
��DE=CD=a��
��CE:CD=2a:a=2��
��CE:CD=![]() ��2��
��2��
��3���ߵ�P���˶��б��֡�APD=90����
���P��·������ADΪֱ����Բ��
��ͼ3����AD���е�ΪQ������CQ���ӳ���Բ���ڵ�P��
��ʱCP�ij������
����Rt��QDC�� ![]()
��![]() ��
��
���߶�CP�����ֵ��![]() .
.