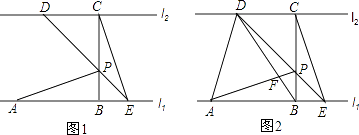题目内容
【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在![]() 上找一点P,使点P到
上找一点P,使点P到![]() 和
和![]() 的距离相等;
的距离相等;
②在射线![]() 上找一点Q,使
上找一点Q,使![]() .
.
(2)在(1)中连接![]() 与
与![]() ,试说明
,试说明![]() 是直角三角形.
是直角三角形.

【答案】(1)①详见解析;②详见解析;(2)详见解析.
【解析】
(1)根据网格特点作出∠A的角平分线与BC的交点就是点P,作BC的垂直平分线与AP的交点就是点Q.
(2)首先利用勾股定理计算出CQ2、BQ2、BC2,然后利用勾股定理逆定理可得△CBQ是直角三角形.
(1)点P就是所要求作的到AB和AC的距离相等的点,点Q就是所要求作的使QB=QC的点.
(2)连接CQ、BQ.
∵CQ2=12+52=26,BQ2=12+52=26,BC2=62+42=36+16=52,∴CQ2+BQ2=BC2,∴∠CQB=90°,∴△CBQ是直角三角形.


练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目