题目内容
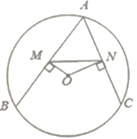
【题目】如图,点A、B、C在半径为2的圆O上,且∠BAC=60°,作OM⊥AB于点M,ON⊥AC于点N,连接MN,则MN的长为( )
A. 1B. ![]() C. 2D. 2
C. 2D. 2![]()
【答案】B
【解析】
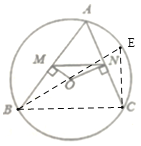
连接OB并延长交圆O于E,则BE为圆O直径,连接BC、CE,由圆周角定理可得∠BEC=60°,由BE是直径可知∠BCE=90°,利用∠BEC的余弦值可得BC的长,根据垂径定理可得AM=BM,AN=CN,即可证明MN是△ABC的中位线,根据三角形中位线定理即可求出MN的长.
连接OB并延长交圆O于E,则BE为圆O直径,连接BC、CE,
∵∠BAC和∠AEC都是![]() 所对圆周角,
所对圆周角,
∴∠BAC=∠BEC=60°,
∵BE是直径,
∴∠BCE=90°,BE=4,
∴BC=BE![]() sin60°=4×
sin60°=4×![]() =2
=2![]() ,
,
∵OM⊥AB,ON⊥AC,
∴AM=BM,AN=CN,
∴MN是△ABC的中位线,
∴MN=![]() BC=
BC=![]() .
.
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目