题目内容
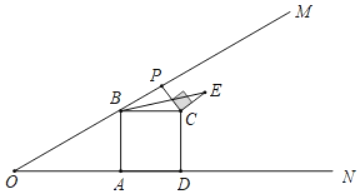
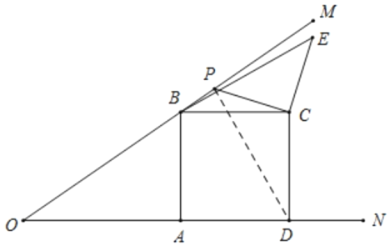
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为( )
A. ![]() +1B. 2
+1B. 2![]() ﹣1C. 3D. 4﹣
﹣1C. 3D. 4﹣![]()
【答案】A
【解析】
连接PD,依据SAS构造全等三角形,即△BCE≌△DCP,将BE的长转化为PD的长,再依据垂线段最短得到当DP最短时,BE亦最短,根据∠O=30°,OD=2+2![]() ,即可求得DP的长的最小值.
,即可求得DP的长的最小值.
解:如图,连接PD,
由题意可得,PC=EC,∠PCE=90°=∠DCB,BC=DC,
∴∠DCP=∠BCE,
在△DCP和△BCE中,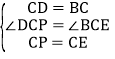 ,
,
∴△DCP≌△BCE(SAS),
∴PD=BE,
当DP⊥OM时,DP最短,此时BE最短,
∵∠AOB=30°,AB=2=AD,
∴OD=OA+AD=2![]() +2,
+2,
∴当DP⊥OM时,DP=![]() OD=
OD=![]() +1,
+1,
∴BE的最小值为![]() +1.
+1.
故选:A.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目