题目内容
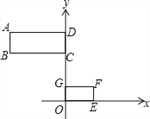
【题目】如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)
(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由
(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;
(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.

【答案】(1)![]() ;(2)S=t2﹣2t+8(0<t<2);(3)
;(2)S=t2﹣2t+8(0<t<2);(3)![]() .
.
【解析】
由题意可得:由运动知,DP=t,AQ=2t,得出AP=4-t,BQ=4-2t,
(1)判断出AQ=AP,得出2t=4-t,即可;
(2)直接利用面积的和差即可得出结论;
(3)先判断![]() =
=![]() ,再得到
,再得到![]() ,从而得出
,从而得出![]() 解方程即可得出结论.
解方程即可得出结论.
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,
由运动知,DP=t,AQ=2t,
∴AP=4﹣t,BQ=4﹣2t,
(1)连接BD,如图1,
∵AB=AD,
∴∠ABD=∠ADB,
∵PQ∥BD,
∴∠ABD=∠AQP,∠APQ=∠ADB,
∴∠APQ=∠AQP,
∴AQ=AP,
∴2t=4﹣t,
∴t=![]() ;
;
(2)S=S正方形ABCD﹣S△APQ﹣S△BCQ﹣S△CDP
=AB2﹣![]() AQ×AP﹣
AQ×AP﹣![]() BQ×BC﹣
BQ×BC﹣![]() DP×CD
DP×CD
=16﹣![]() ×2t×(4﹣t)﹣
×2t×(4﹣t)﹣![]() ×(4﹣2t)×4﹣
×(4﹣2t)×4﹣![]() t×4
t×4
=16+t2﹣4t﹣8+4t﹣2t
=t2﹣2t+8(0<t<2);
(3)如图2,
过点C作CN⊥PQ于N,
∴S△MCQ=![]() MQ×CN,S△MCP=
MQ×CN,S△MCP=![]() MP×CN,
MP×CN,
∵S△QCM:S△PCM=3:5,
∴![]() =
=![]() ,
,
∴![]() ,
,
过点M作MG⊥AB于G,MH⊥AD于H,
∵点M是正方形ABCD的对角线AC上的一点,
∴MG=MH,
∴S△AMQ=![]() AQ×MG,S△APM=
AQ×MG,S△APM=![]() AP×MH,
AP×MH,
∴![]()
∴![]()
∴t=![]() .
.

【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人数记为![]() ,请用
,请用![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?
【题目】为了了解学校开展“孝敬父母,从家务劳动做起”活动的实施情况,该校抽取八年级50名学生,调查他们一周(按七天计算)做家务所用时间(单位:小时)得到一组数据,绘制成下表:
时间x(小时) | 划记 | 人数 | 所占百分比 |
0.5x≤x≤1.0 | 正正 | 14 | 28% |
1.0≤x<1.5 | 正正正 | 15 | 30% |
1.5≤x<2 |
| 7 |
|
2≤x<2.5 |
| 4 | 8% |
2.5≤x<3 | 正 | 5 | 10% |
3≤x<3.5 |
| 3 |
|
3.5≤x<4 |
|
| 4% |
合计 | 50 | 100% |
(1)请填表中未完成的部分;
(2)根据以上信息判断,每周做家务的时间不超过1.5小时的学生所占的百分比是多少?
(3)针对以上情况,写出一个20字以内的倡导“孝敬父母,热爱劳动”的句子.