Question

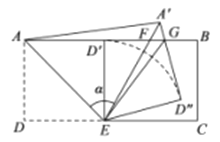
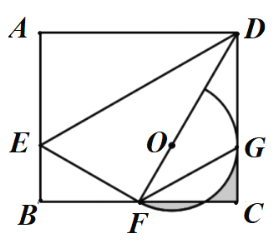
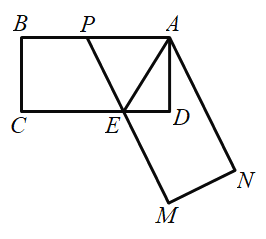
【题目】如图，在矩形中，，，点为边上的一点（与、不重合）四边形关于直线的对称图形为四边形，延长交与点，记四边形的面积为．

（1）若，求的值；

（2）设，求关于的函数表达式．

Answer 1

【答案】（1）；（2）

【解析】

（1）解Rt△ADE可得和AE的长，然后根据平行线的性质、对称的性质可得，进而可判断为等边三角形，再根据S=S△APE+S△ADE解答即可；

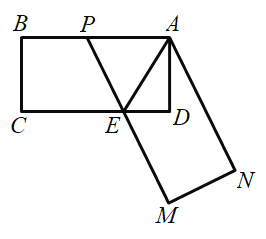
（2）过点作于点F，如图，则四边形ADEF是矩形，由（1）得，从而可得，设，则，然后在中根据勾股定理即可利用x表示a，然后根据S=S△APE+S△ADE即可求出结果．

解：（1）在Rt△ADE中，∵，，

∴，∴，

∴，

∵，∴，

∵四边形关于直线的对称图形为四边形，

∴，

∵，

∴，

∴为等边三角形，

∴S=S△APE+S△ADE=；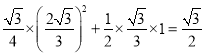

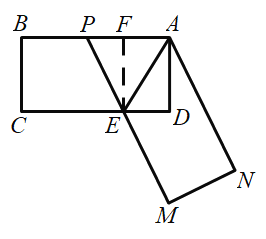
（2）过点作于点F，如图，则四边形ADEF是矩形，

∴，，

由（1）可知，，

∴，

设，则，

在中，由勾股定理，得：，解得：，

∴S=S△APE+S△ADE=．