Question

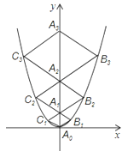
【题目】二次函数y=x2的图象如图，点A0位于坐标原点，点A1，A2，A3…An在y轴的正半轴上，点B1，B2，B3…Bn在二次函数位于第一象限的图象上，点C1，C2，C3…Cn在二次函数位于第二象限的图象上，四边形A0B1A1C1，四边形A1B2A2C2，四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形，∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°，菱形A2019B2020A2020C2020的周长为________．

Answer 1

【答案】8080

【解析】

由于△A0B1A1，△A1B2A2，△A2B3A3，…，都是等边三角形，因此∠B1A0x＝30°，可先设出△A0B1A1的边长，然后表示出B1的坐标，代入抛物线的解析式中即可求得△A0B1A1的边长，用同样的方法可求得△A0B1A1，△A1B2A2，△A2B3A3，…的边长，然后根据各边长的特点总结出此题的一般化规律，根据菱形的性质易求菱形An1BnAnCn的周长．

∵四边形A0B1A1C1是菱形，∠A0B1A1＝60°，

∴△A0B1A1是等边三角形．

设△A0B1A1的边长为m1，则B1的纵坐标为，利用勾股定理求出B1的横坐标为，

∴B（，）；

代入抛物线的解析式中得：，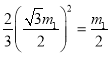

解得m1＝0（舍去），m1＝1；

故△A0B1A1的边长为1，

设△A1B2A2的边长为m2，则B2的纵坐标为+1，利用勾股定理求出B2的横坐标为，

∴B（，+1）；

代入抛物线的解析式中得：，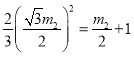

解得m2＝-1（舍去），m2＝2；

故△A1B2A2的边长为2，

同理可求得△A2B3A3的边长为3，

…

依此类推，等边△An1BnAn的边长为n，

故菱形An1BnAnCn的周长为4n．

∴菱形A2019B2020A2020C2020的周长为4×2020=8080，

故答案是：8080．