Question

【题目】二次函数的图像过点，且与轴交于点，点在该抛物线的对称轴上，若是以为直角边的直角三角形，则点的坐标为__________．

Answer 1

【答案】或

【解析】

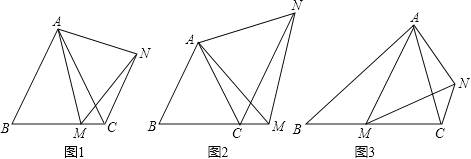
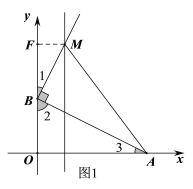
先求出点B的坐标和抛物线的对称轴，然后分两种情况讨论：当∠ABM=90°时，如图1，过点M作MF⊥y轴于点F，易证△BFM∽△AOB，然后根据相似三角形的性质可求得BF的长，进而可得点M坐标；当∠BAM=90°时，辅助线的作法如图2，同样根据△BAE∽△AMH求出AH的长，继而可得点M坐标．

解：对，当x=0时，y=3，∴点B坐标为（0，3），

抛物线的对称轴是直线：，

当∠ABM=90°时，如图1，过点M作MF⊥y轴于点F，则，

∵∠1+∠2=90°，∠2+∠3=90°，

∴∠1=∠3，

又∠MFB=∠BOA=90°，

∴△BFM∽△AOB，

∴，即，解得：BF=3，

∴OF=6，

∴点M的坐标是（，6）；

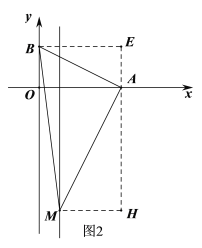
当∠BAM=90°时，如图2，过点A作EH⊥x轴，过点M作MH⊥EH于点H，过点B作BE⊥EH于点E，则，

同上面的方法可得△BAE∽△AMH，

∴，即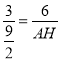，解得：AH=9，

∴点M的坐标是（，﹣9）；

综上，点M的坐标是或．

故答案为：或．