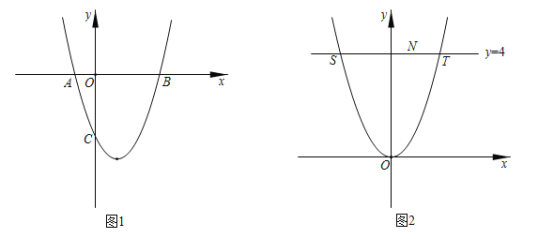��Ŀ����
����Ŀ����֪���κ���y��ax2+bx+c�е�y��x�IJ��ֶ�Ӧֵ���±���
x | ��1 | 0 | 1 | 3 |
y | ��3 | 1 | 3 | 1 |
���н����У��������ߵĿ������£�����ͼ��ĶԳ���Ϊx��1������x��1ʱ������ֵy��x�����������������ax2+bx+c��0��һ��������4������ax12+bx1��ax22+bx2����x1��x2����x1+x2��3��������ȷ�Ľ�����(����)
A.�٢ڢ�B.�٢ڢۢܢ�C.�٢ۢ�D.�٢ۢܢ�
���𰸡�C
��������
���������ߵĶԳ��Եõ������ߵĶԳ���Ϊֱ��x=![]() ����ɶԢڽ����жϣ����ú���ֵ�ı仯��ȷ�������߿������£���ɶԢٽ����жϣ����ݶ��κ��������ʶԢ۽����жϣ����������ߵĶԳ���ȷ����������x���һ�������ڣ�3��0���ͣ�4��0��֮�䣬��ɶԢܽ����жϣ�
����ɶԢڽ����жϣ����ú���ֵ�ı仯��ȷ�������߿������£���ɶԢٽ����жϣ����ݶ��κ��������ʶԢ۽����жϣ����������ߵĶԳ���ȷ����������x���һ�������ڣ�3��0���ͣ�4��0��֮�䣬��ɶԢܽ����жϣ�
�⣺�ɱ����֪���ɱ����֪��x��0��x��3ʱ������ֵy����1��
�������ߵĶԳ���Ϊֱ��![]() ��
��
��x��![]() ʱ�����κ���y��ax2+bx+cȡ�����ֵ��
ʱ�����κ���y��ax2+bx+cȡ�����ֵ��
�������ߵĿ������£�������ȷ��������
��x��![]() ʱ��y��x���������������ȷ��
ʱ��y��x���������������ȷ��
����ax2+bx+c��0��һ�������ک�1��С��0���̵���һ��������3��С��4����������
��ax12+bx1��ax22+bx2����x1��x2����![]() ��
��
��x1+x2��3��������ȷ��
��ѡ��C��

 ��У����ϵ�д�
��У����ϵ�д�