题目内容
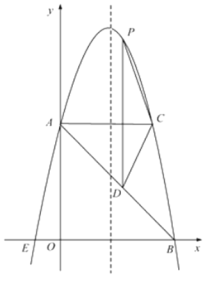
【题目】如图1，抛物线
：
交
轴于点
，
，交
轴于点
.
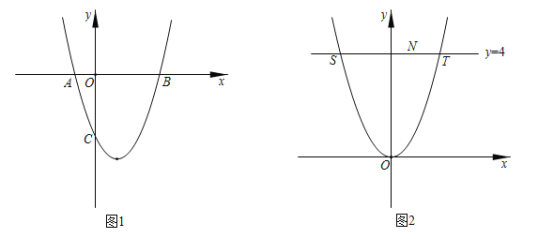
（1）直接写出当
时，的取值范围是____________；
（2）点
在抛物线上，求
的面积；
（3）如图2，将抛物线平移，使其顶点为原点
，得到抛物线
，直线
与抛物线交于
、
两点，点
是线段
上一动点（不与、重合），试探究抛物线上是否存在点
，点关于点的中心对称点
也在抛物线上.
【答案】（1）
或
；（2）6；（3）抛物线
上存在点
，点关于点
的中心对称点
也在抛物线上，理由见解析
【解析】
（1）由抛物线与坐标轴的交点坐标，依据函数图象即可写出y＞0时x的取值范围；
（2）求出P点坐标为（4，5），可求出直线PC的解析式，求出直线PC与x轴的交点坐标D（
，0），由S△PCB=S△BDC+S△BDP可求出答案；
（3）由题意得抛物线C1的解析式为y=x2，设N（a，4），且-2＜a＜2，设R（m，m2），由中心对称的性质可表示K点的坐标，则得到关于m的方程，由此可判断结论．
解：（1）∵抛物线与y轴交于（0，-3），与x轴交于B（3，0），A（-1，0），
∴当y＞0时，x的取值范围为x＞3或x＜-1．
故答案为：或.
（2）将
代入抛物线
：
中，
∴16-8-3=m，
∴
，
∴
，
设直线PC的解析式为y=kx+b，
∴
，
解得
∴直线PC的解析式为y=2x-3
当y=0时，x= ，
∴直线
：
，则直线与
轴的交点为
，
∴DB=
∴
.
（3）依题意得抛物线：
，设
，抛物线：上存在点
，则点关于点成中心对称的点的坐标为
，
当
在抛物线：上，
∴
，
∴得到关于
的一元二次方程
，
∴
，
∵
，
∴
，
∴关于的一元二次方程有两个不相等的实数根.
∴抛物线上存在点，点关于点的中心对称点也在抛物线上
【题目】二次函数
（
是常数，
）的自变量
与函数值
的部分对应值如下表：
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当
时，与其对应的函数值
．有下列结论：①
；②
和3是关于的方程
的两个根；③
．其中，正确结论的个数是（ ）
A. 0B. 1C. 2D. 3
【题目】已知二次函数y＝ax2+bx+c中的y与x的部分对应值如下表：
x | ﹣1 | 0 | 1 | 3 |
y | ﹣3 | 1 | 3 | 1 |
下列结论中：①抛物线的开口向下；②其图象的对称轴为x＝1；③当x＜1时，函数值y随x的增大而增大；④方程ax2+bx+c＝0有一个根大于4；⑤若ax12+bx1＝ax22+bx2，且x1≠x2，则x1+x2＝3，其中正确的结论有( )
A.①②③B.①②③④⑤C.①③⑤D.①③④⑤
