题目内容
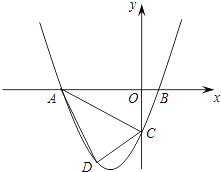
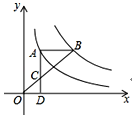
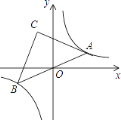
【题目】如图,在反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,若tan∠CAB=2,则k的值为( )
的图象上运动,若tan∠CAB=2,则k的值为( )
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
【答案】B
【解析】
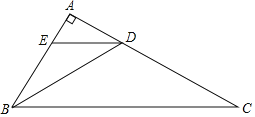
连接OC,过点A作AE⊥x轴于点E,过点C作CF⊥y轴于点F,通过同角的余角相等得出∠AOE=∠COF,结合“∠AEO=90°,∠CFO=90°”可得出△AOE∽△COF,根据相似三角形的性质得出比例式,再由tan∠CAB=2,可得出CFOF的值,进而得到k的值.
解:如图,连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥y轴于点F,
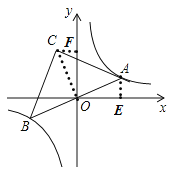
∵直线AB过点O,点A、B在反比例函数y=![]() 的图像上,
的图像上,
∴点A、B点关于O点对称,
∴AO=BO.
又∵AC=BC,
∴CO⊥AB.
∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE∽△COF,
∴![]() =
=![]() =
=![]() ,
,
∵tan∠CAB=![]() =2,
=2,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴CF=2AE,OF=2OE.
又∵AEOE=![]() ,
,
∴CFOF=|k|=4 AEOE=6,
∴k=±6.
∵点C在第二象限,
∴k=-6,
故选:B.

【题目】八(2)班分成甲、乙两组进行一分钟投篮测试,并规定得6分及以上为合格,得9分及以上为优秀,现两组学生的一次测试成绩统计如下表:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组人数(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组人数(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上表数据,把下面的统计表补充完整,并写出求甲组平均分的过程;
统计量 | 平均分 | 方差 | 众数 | 中位数 | 合格率 | 优秀率 |
甲组 |
| 2.56 |
| 6 | 80.0% | 26.7% |
乙组 | 6.8 | 1.76 | 7 |
| 86.7% | 13.3% |
(2)如果从投篮的稳定性角度进行评价,你认为哪组成绩更好?并说明理由;
(3)小聪认为甲组成绩好于乙组,请你说出支持小聪观点的理由;