题目内容
【题目】我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”．
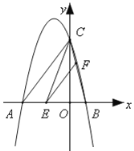
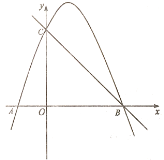
(1)求抛物线y＝x2﹣2x+2与x轴的“和谐值”；
(2)求抛物线y＝x2﹣2x+2与直线y＝x﹣1的“和谐值”．
【答案】(1)抛物线y＝x2﹣2x+2与x轴的“和谐值”为1；(2)抛物线y＝x2﹣2x+3与直线y＝x﹣1的“和谐值”为
．
【解析】
（1）根据题意将抛物线化成顶点式，找到函数最值即可求解；（2）取P点为抛物线y＝x2﹣2x+2任意一点，作PQ∥y轴交直线y＝x﹣1于Q，分析PQ的长度，得到二次函数解析式，求其顶点坐标即可.
(1)∵y＝(x﹣1)2+1，
∴抛物线上的点到x轴的最短距离为1，
∴抛物线y＝x2﹣2x+2与x轴的“和谐值”为1；
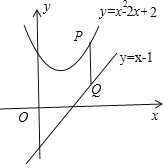
(2)如图，P点为抛物线y＝x2﹣2x+2任意一点，作PQ∥y轴交直线y＝x﹣1于Q，
设P(t，t2﹣2t+2)，则Q(t，t﹣1)，
∴PQ＝t2﹣2t+2﹣(t﹣1)＝t2﹣3t+3＝(t﹣
)2+，
当t＝时，PQ有最小值，最小值为，
∴抛物线y＝x2﹣2x+3与直线y＝x﹣1的“和谐值”为．
练习册系列答案
相关题目
【题目】已知二次函数y＝ax2+bx+c中的y与x的部分对应值如下表：
x | ﹣1 | 0 | 1 | 3 |
y | ﹣3 | 1 | 3 | 1 |
下列结论中：①抛物线的开口向下；②其图象的对称轴为x＝1；③当x＜1时，函数值y随x的增大而增大；④方程ax2+bx+c＝0有一个根大于4；⑤若ax12+bx1＝ax22+bx2，且x1≠x2，则x1+x2＝3，其中正确的结论有( )
A.①②③B.①②③④⑤C.①③⑤D.①③④⑤
